Cechy podzielności liczb przez 2, 4, 8 jedni kochają, inni nienawidzą! Poniżej zmierzymy się z tematem. Pokażę Tobie na wielu przykładach kiedy podana liczba dzieli się przez 2 lub 4 lub 8 i jak to szybko zauważyć. Jeśli po przeczytaniu nadal nie wiesz jak ten temat ugryźć, możesz zawsze skorzystać z filmów na YouTube.

Przeskocz do liczby, której podzielność Ciebie interesuje 2 lub 4 lub 8.

Cechy podzielności liczb przez 2.

Liczba jest podzielna przez 2, gdy jest liczbą parzystą, czyli jej ostatnią cyfrą jest: 0,2,4,6,8.

Jeszcze raz liczba parzysta jest ZAWSZE podzielna przez 2.

ZAWSZE, ZAWSZE, ZAWSZE!

Nie ma wyjątku.

ZAWSZE!

Dlaczego każda liczba parzysta jest podzielna przez 2?

Wypiszmy kilka liczb parzystych:

4, 14, 24, 32, 36, 38, 54, 98, 124, 568, 2572 itd.

Teraz każdą z tych liczb zapiszmy za pomocą iloczynu liczby 2. Ups.. no dobra zgrywam się, powiem to po ludzku: zapiszmy za pomocą mnożenia 2 * jakaś liczba.

I widzisz w każdym mnożeniu mamy liczbę 2 razy coś tam. Dwójkę zaznaczyłam na żółto na powyższym zdjęciu. I jak to się dzieję, że każda z tych liczb dzieli się przez dwa?

Te dwójki się skrócą ( dwójki zaznaczyłam na różowo) i w ten sposób widzimy, że każda liczba parzysta podzieli się przez dwa, bo składa się z mnożenia 2 * liczba.

liczba podzielna przez 2 to liczba parzysta.

Przypominajka!

Zadanie.

Sprawdź czy podana liczba jest podzielna przez 2. Inaczej mówiąc, która z poniższych liczb jest liczbą parzystą.

2, 11, 64, 764, 124, 75, 8793, 7222, 89067421, 3412, 541, 9870.

Odpowiedź:

Sprawdźmy, która z tych liczba ma 0,2,4,6,8 na końcu.

2, 11, 64, 764, 124, 75, 8793, 7222, 89067421, 3412, 541, 9870.

• Liczbami podzielnymi przez dwa są: 2, 64, 764, 124, 7222, 3412, 9870, bo mają 0 lub 2 lub 4 lub 6 lub 8 na końcu.
• Liczbami nie podzielnymi przez dwa są: 11, 75, 8793, 89067421, 541, bo NIE mają 0 lub 2 lub 4 lub 6 lub 8 na końcu.

Zobacz więcej przykładów na youtube KLIK.

Cechy podzielności liczb przez 4.

Liczba jest podzielna przez 4, jeśli jej dwie ostatnie cyfry tworzą liczbę podzielną przez 4.

Jakie liczby dwucyfrowe są podzielne przez 4?

Liczby dwucyfrowe podzielne przez 4 to: 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96.

Jak zobaczysz liczbę, która na końcu ma którąś z tych liczb: 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96 to znaczy, że jest podzielna przez 4.

liczba podzielna przez 4 to liczba parzysta oraz jej dwie ostatnie cyfry tworzą liczbę podzielną przez 4.

Przypominajka!

Zadanie.

Sprawdź czy podana liczba jest podzielna przez 4.

124, 345, 4568, 5741, 980765, 90080032.

Odpowiedź.

Zaznaczyłam dwie ostatnie cyfry z naszych liczb.

• 124
  • Dwie ostatnie cyfry to 24.
  • 24 jest podzielne przez 4, więc liczba 124 jest podzielna przez 4.
• 345,
  • Dwie ostatnie cyfry to 45.
  • 45 nie jest podzielne przez 4, więc liczba 345 nie jest podzielna przez 4.
• 4568,
  • Dwie ostatnie cyfry to 68.
  • 68 jest podzielne przez 4, więc liczba 4568 jest podzielna przez 4.
• 5741,
  • Dwie ostatnie cyfry to 41.
  • 41 nie jest podzielne przez 4, więc liczba 5741 nie jest podzielna przez 4.
• 980765,
  • Dwie ostatnie cyfry to 65.
  • 65 nie jest podzielne przez 4, więc liczba 980765 nie jest podzielna przez 4.
• 90080032,
  • Dwie ostatnie cyfry to 32.
  • 32 jest podzielne przez 4, więc liczba 90080032 jest podzielna przez 4.

I kolejna dawka przykładów kiedy liczba jest podzielna przez 4 KLIK NA YouTube.

Cechy podzielności liczb przez 8.

Liczba jest podzielna przez 8, jeśli jej trzy ostatnie cyfry tworzą liczbę podzielną przez 8.

Liczby podzielne przez 8 są to też liczby parzyste.

Łącząc wszystko:

liczba podzielna przez 8 to liczba parzysta oraz jej trzy ostatnie cyfry tworzą liczbę podzielną przez 8.

Przypominajka!

No to popatrzmy najpierw jakie liczby dwucyfrowe dzielą się przez 8?

8 16 24 32 40 48 56 64 72 80 88 96

Tylko takie. Nie jest ich dużo.

Teraz spójrzmy ile jest liczb trzycyfrowych podzielnych przez 8?

104 112 120 128 136 144 152 160 168 176 184 192
200 208 216 224 232 240 248 256 264 272 280 288
296 304 312 320 328 336 344 352 360 368 376 384
392 400 408 416 424 432 440 448 456 464 472 480
488 496 504 512 520 528 536 544 552 560 568 576
584 592 600 608 616 624 632 640 648 656 664 672
680 688 696 704 712 720 728 736 744 752 760 768
776 784 792 800 808 816 824 832 840 848 856 864
872 880 888 896 904 912 920 928 936 944 952 960
968 976 984 992

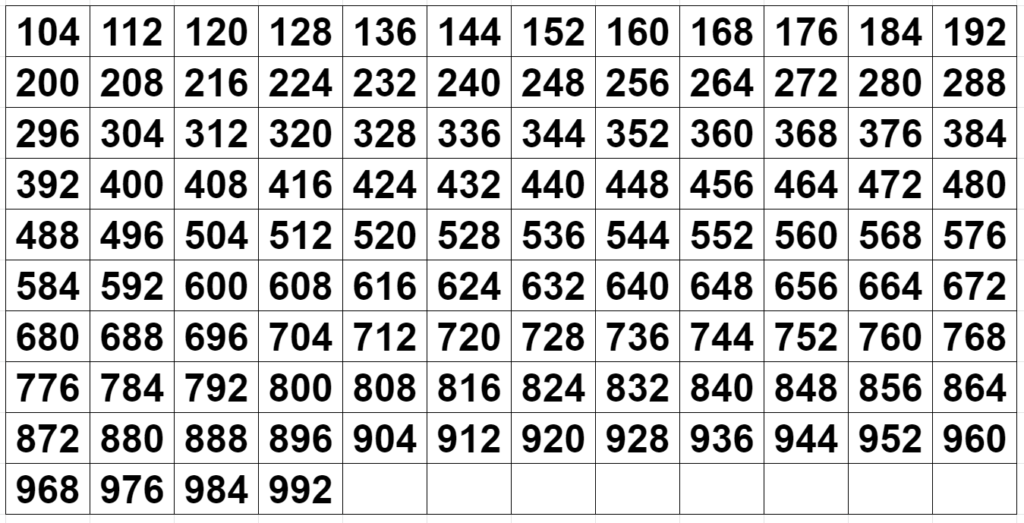
Jak zobaczysz którąś z tych liczb to wiesz, że ona dzieli się przez 8.

Zadanie.

Sprawdź czy podana liczba jest podzielna przez 8.

1720, 345, 4552, 5741, 980920, 90080680, 90080684

Odpowiedź.

Zaznaczyłam dwie ostatnie cyfry z naszych liczb.

• 1720
  • Trzy ostatnie cyfry to 720.
  • 720 jest podzielne przez 8, więc liczba 1720 jest podzielna przez 8.

• 345
  • Trzy ostatnie cyfry to 345.
  • 345 NIE jest podzielne przez 8, więc liczba 345 NIE jest podzielna przez 8.

• 4552
  • Trzy ostatnie cyfry to 552.
  • 552 jest podzielne przez 8, więc liczba 4552 jest podzielna przez 8.

• 5741
  • Trzy ostatnie cyfry to 741.
  • 741 NIE jest podzielne przez 8, więc liczba 5741 NIE jest podzielna przez 8.

• 980920
  • Trzy ostatnie cyfry to 920.
  • 920 jest podzielne przez 8, więc liczba 980920 jest podzielna przez 8.

• 90080680
  • Trzy ostatnie cyfry to 680.
  • 920 jest podzielne przez 8, więc liczba 980920 jest podzielna przez 8.

• 90080684
  • Trzy ostatnie cyfry to 684.
  • 684 NIE jest podzielne przez 8, więc liczba 90080684 NIE jest podzielna przez 8.

I zobacz jak sprawdzam czy liczba jest podzielna przez 8 KLIK.

I to już koniec.

Jeśli jesteś głodny wiedzy to zapraszam do uzupełnienia tematu cech podzielności liczb o :

1. Cechy podzielności przez 3 lub 9.
2. Cechy podzielności przez 5 lub 10.
3. Piguła cech podzielności liczb.