Wykresy i przekształcenia funkcji trygonometrycznych czekają na odkrycie, sinus, cosinus, tangens oraz cotangens – te funkcje odgrywają niebywałą rolę w świecie matematyki. Poprzez analizę ich wykresów, możemy zrozumieć ich zachowanie w różnych kontekstach argumentu. Przekształcenia wykresu, takie jak zmiany skali czy przesunięcia, otwierają przed nami drzwi do głębszego zrozumienia ich unikalnych właściwości. Więc, nie czekajmy dłużej – zanurzmy się w fascynujący świat funkcji trygonometrycznych! Wykresy i przekształcenia funkcji trygonometrycznych czekają na odkrycie!

Co Ciebie czeka w tym wpisie:

1. Wykres funkcji: sinus, cosinus, tangens, cotangens.
2. Przekształcenie funkcji af(x).
3. Przekształcenie funkcji f(ax).
4. Przekształcenie funkcji -f(x) oraz f(-x).
5. Przekształcenie funkcji |f(x)| oraz f(|x|).

Wykresy i przekształcenia wykresu funkcji trygonometrycznych sinus. Jak narysować funkcję sinus?

By zacząć rysować wykres funkcji trygonometrycznej musisz kojarzyć tą tabele:

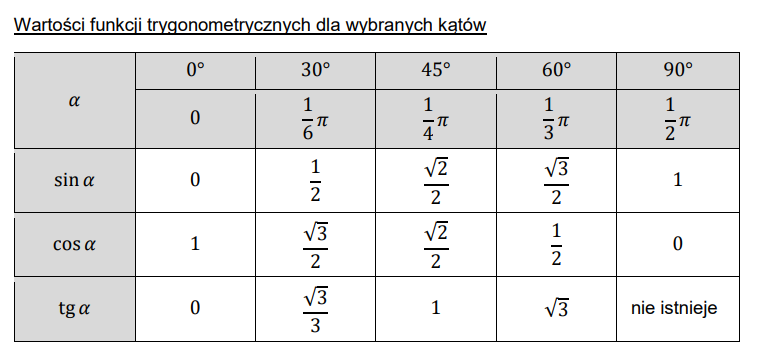
Wróćmy do sinusa. Rysowanie wykresu funkcji sinus jest jednym z podstawowych zadań związanych z analizą funkcji trygonometrycznych. Funkcja sinus jest okresowa i ma wartości z przedziału [-1, 1], co oznacza, że jej wykres będzie wyglądał jak sinusoidalna krzywa przechodząca przez punkty (0,0), (π/2, 1), (π, 0), (3π/2, -1) i tak dalej. Można sobie wyobrazić, że taki wykres reprezentuje oscylację wartości funkcji w określonym czasie. Co więcej, funkcja sinus jest nieparzysta, co oznacza, że jest symetryczna względem osi x=π/2. Ta cecha jest bardzo przydatna w wielu dziedzinach, takich jak fizyka, elektronika i inżynieria, gdzie wykorzystuje się funkcję sinus do opisywania różnego rodzaju oscylacji i fali. Zrozumienie wykresu funkcji sinus jest więc niezwykle ważne dla szeroko pojętej matematyki i nauk ścisłych.

Najlepiej spójrz na poniższy wykres, natomiast jeśli wolisz posłuchać to zapraszam Ciebie na film na YouTubie KLIK DO FILMU.

Wykresy i przekształcenia wykresu funkcji trygonometrycznych cosinus. Jak rysować wykres funkcji cosinus?

Wykres funkcji cosinus jest równie ważny jak wykres funkcji sinus, ponieważ funkcja cosinus jest blisko powiązana z funkcją sinus. Podobnie jak funkcja sinus, funkcja cosinus jest okresowa i ma wartości z przedziału [-1, 1]. Różnicą między tymi dwoma funkcjami jest to, że wykres funkcji cosinus jest symetryczny względem osi y=0, co oznacza, że jest funkcją parzystą. Funkcja cosinus jest często używana do opisywania różnego rodzaju zjawisk związanych z kątami i promieniami, takich jak np. kąt padania światła czy kąt nachylenia powierzchni względem płaszczyzny. Zrozumienie wykresu funkcji cosinus jest więc kluczowe dla zrozumienia wielu zagadnień z dziedzin takich jak geometria, fizyka i astronomia.

I spójrz jak ten wykres wygląda. Dokładnie i szczegółowo pokazuję w filmie na YouTubie o tutaj klik.

Wykresy i przekształcenia wykresu funkcji trygonometrycznych -tangens. Jak rysować wykres funkcji tangens?

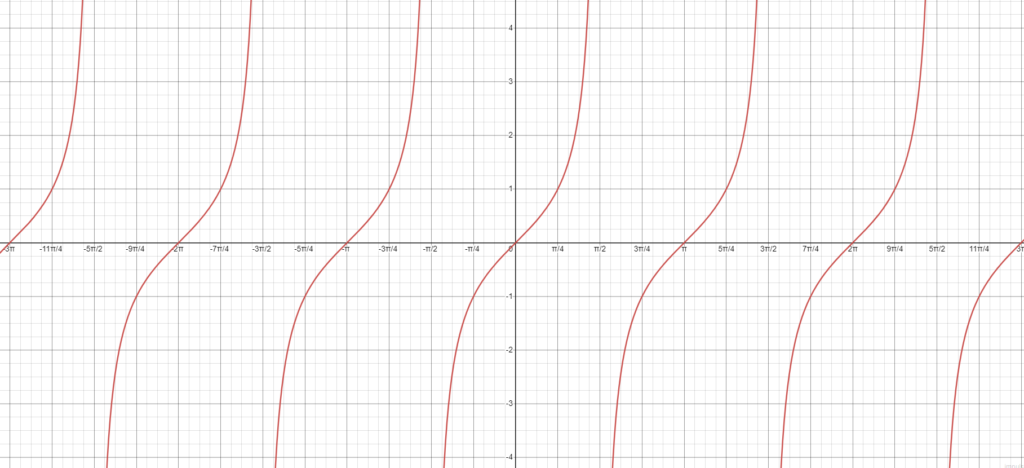
Wykres funkcji tangens jest jednym z najbardziej interesujących wykresów funkcji trygonometrycznych, ponieważ jego kształt jest bardzo zróżnicowany i może przybierać różne formy w zależności od zakresu argumentów.

Funkcja tangens jest okresowa i nie jest ani parzysta, ani nieparzysta, co oznacza, że jej wykres nie jest symetryczny względem żadnej z osi.

Wartości funkcji tangens są zdefiniowane dla każdego argumentu z wyjątkiem liczb których wartość jest wielokrotnością π/2. W tych punktach funkcja tangens nie ma wartości i jest oznaczana jako nieoznaczona.

Zrozumienie wykresu funkcji tangens jest więc bardzo ważne dla zrozumienia wielu zagadnień z dziedzin takich jak matematyka, fizyka czy inżynieria, gdzie funkcja tangens jest często wykorzystywana do opisywania różnego rodzaju zależności i proporcji.

Teraz spójrz jak wygląda wykres funkcji tangens:

Wykresy i przekształcenia wykresu funkcji trygonometrycznych – cotangens. Jak rysować wykres funkcji cotangens?

Funkcja cotangens jest bliźniaczą funkcją do tangens. W zasadzie, jej wykres jest „odwrócony” względem osi poziomej względem wykresu tangens. To znaczy, że tam, gdzie tangens ma duże wartości, cotangens ma małe i na odwrót.

Funkcja cotangens jest okresowa i ma wartości z przedziału (-∞, ∞). Wartości funkcji cotangens są zdefiniowane dla każdego argumentu z wyjątkiem liczb których wartość jest wielokrotnością π. W tych punktach funkcja cotangens nie ma wartości i jest oznaczana jako nieoznaczona.

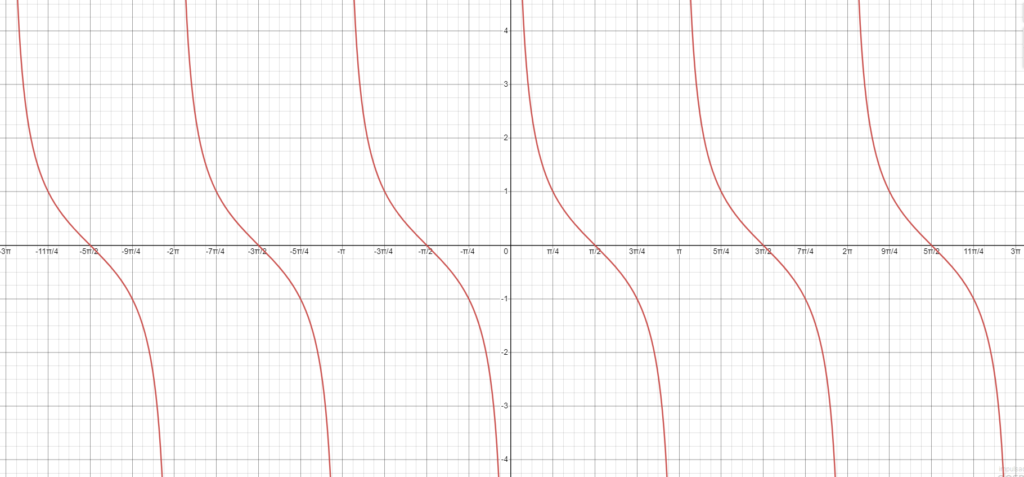
Możesz zobaczyć też jak tworzę wykres funkcji tangens i cotangens w filmie na youtube o TUTAJ.

Przekształcenie funkcji af(x) asinx, acosx, atgx, actgx.

Szybkie przypomnienie o tym co to jest za przekształcenie g(x)=af(x). Aby z wykresu f(x) otrzymać g(x) dany wykres albo trzeba spłaszczyć albo wyciągnąć. Wszystko robimy „po osi y”, wartości na osi x nie ruszamy. Spójrz na przykład.

Jeśli ta liczba przed f(x) jest większa od 0 a mniejsza od 1, to wykres spłaszczamy. O tak:

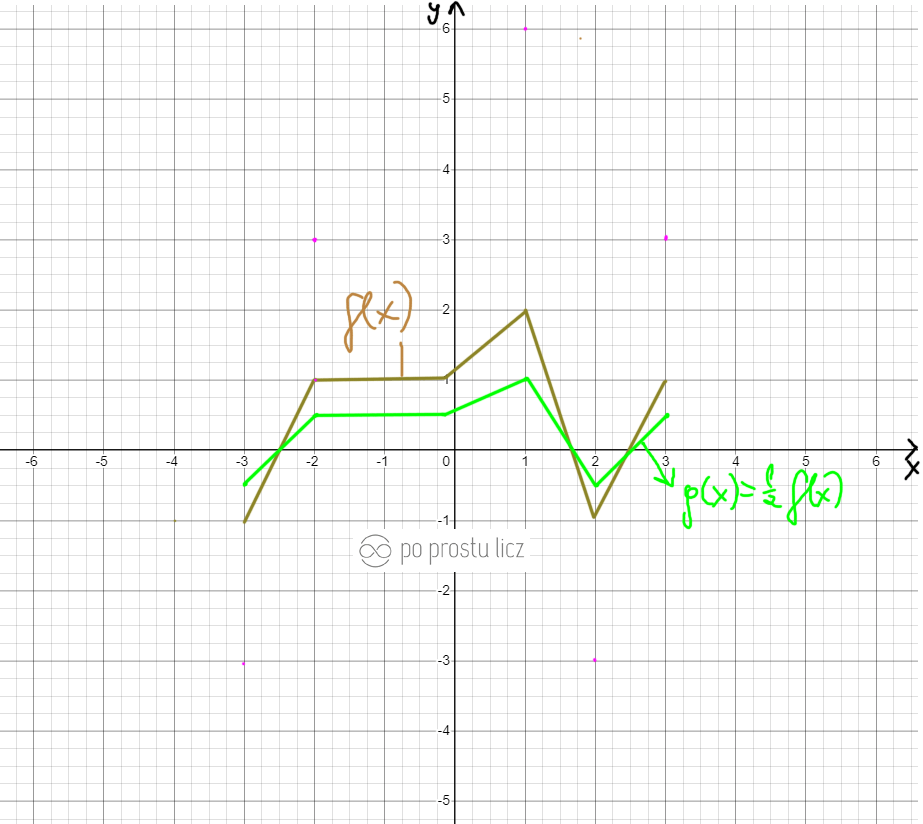
Natomiast gdy a jest większe od 1 rozciągamy. O tak:

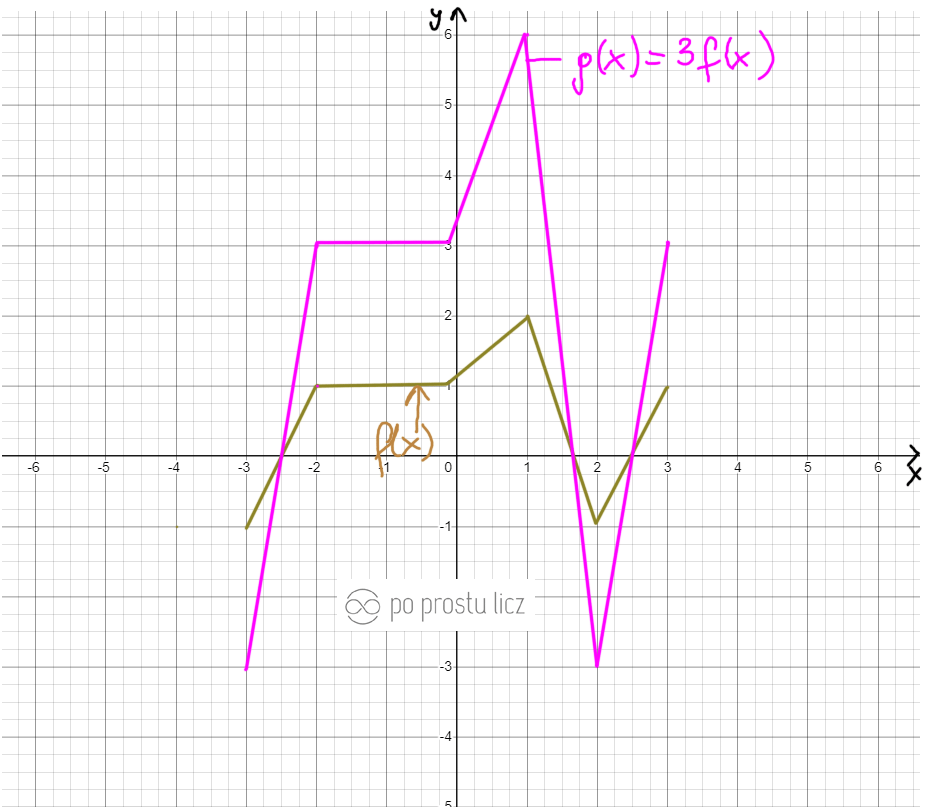
To teraz lecimy z funkcjami trygonometrycznymi.

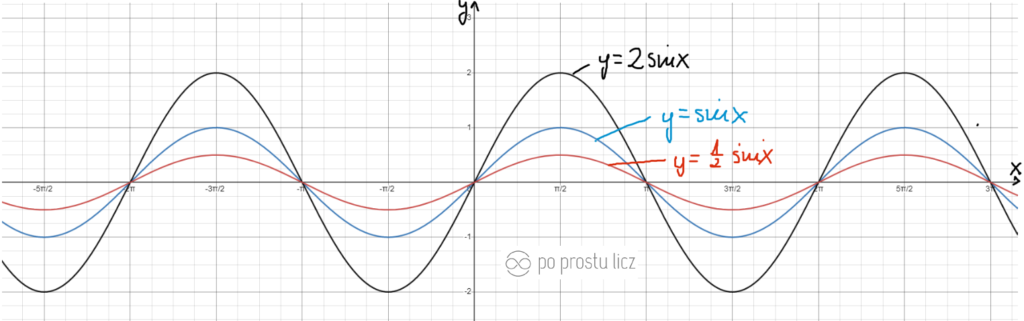
Wykres funkcji f(x)=2sinx oraz f(x)=1/2sinx.

• Niebieski to f(x)=sinx.
• Czarny to f(x)=2sinx.
• Czerwony to f(x)=1/2sinx.

Zobacz film dotyczący przekształceń funkcji sinus i cosinus. O kliknij tutaj i przenieś się na YOUTUBE.

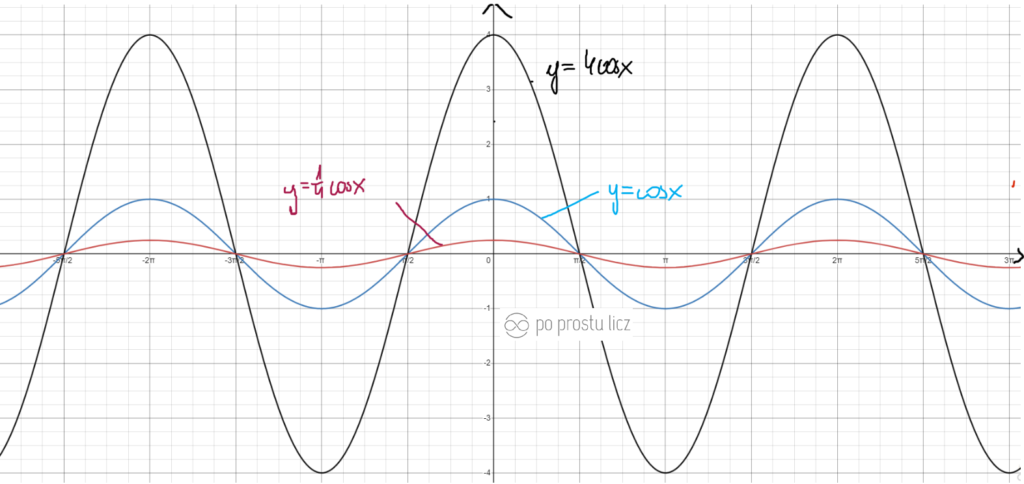
Wykres funkcji f(x)=4cosx oraz f(x)=1/4cosx.

• Niebieski to f(x)=cosx.
• Czarny to f(x)=4cosx.
• Czerwony to f(x)=1/4cosx.

Wolisz posłuchac? Zobacz 4 dodatkowe przykłady jakie dla Ciebie przygotowałam na youtube. KLIK W YOUTUBE.

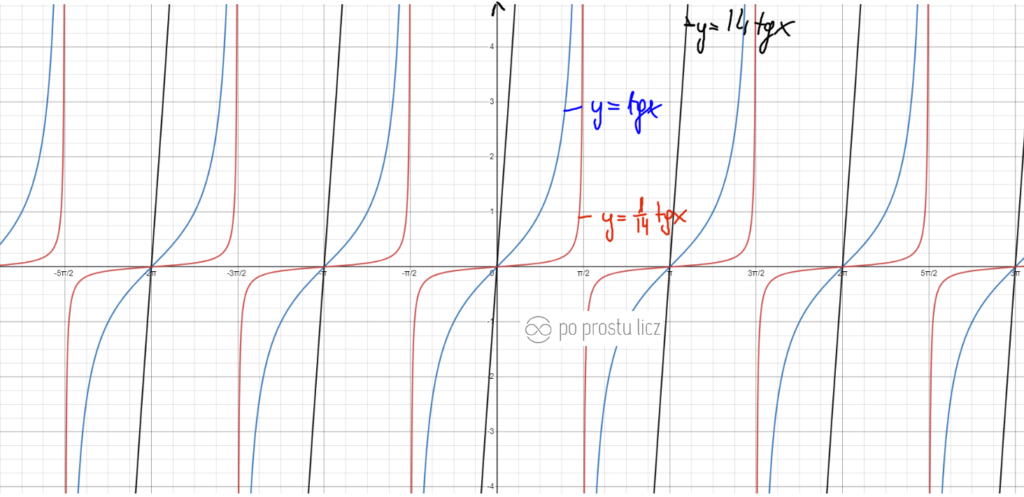
Wykres funkcji f(x)=14tgx oraz f(x)=1/14tgx.

• Niebieski to f(x)=tgx.
• Czarny to f(x)=14tgx. – im większa liczba przed tangensem tym bardziej wykres przypomina prostą kreskę
• Czerwony to f(x)=1/14tgx. im większa liczba w mianowniku tym większą półkę ma tangens 😀 zerknij w film poniżej tam pokazuję dokładnie co i jak.

Wolisz posłuchać i zobaczyć więcej przykładów związanych z tymi przekształceniami zapraszam do poniższego filmu. SKOK DO FILMU.

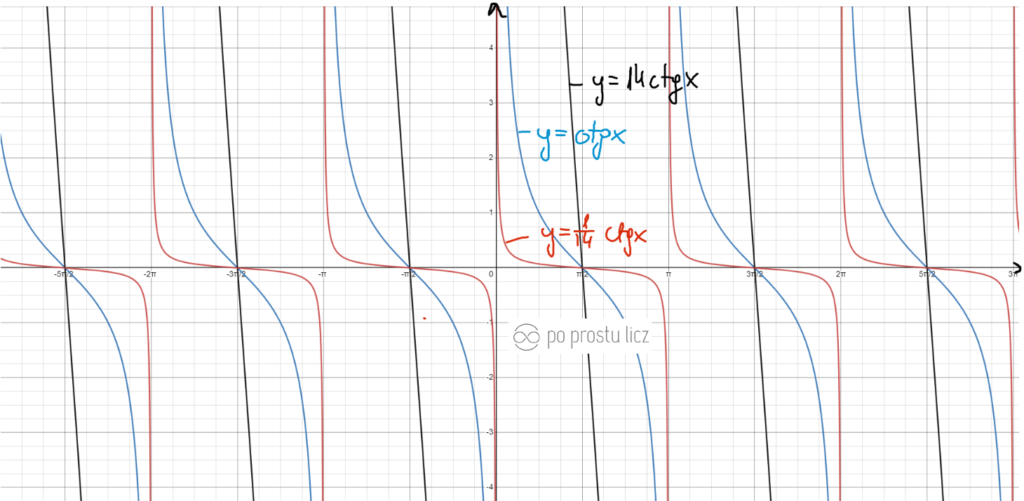
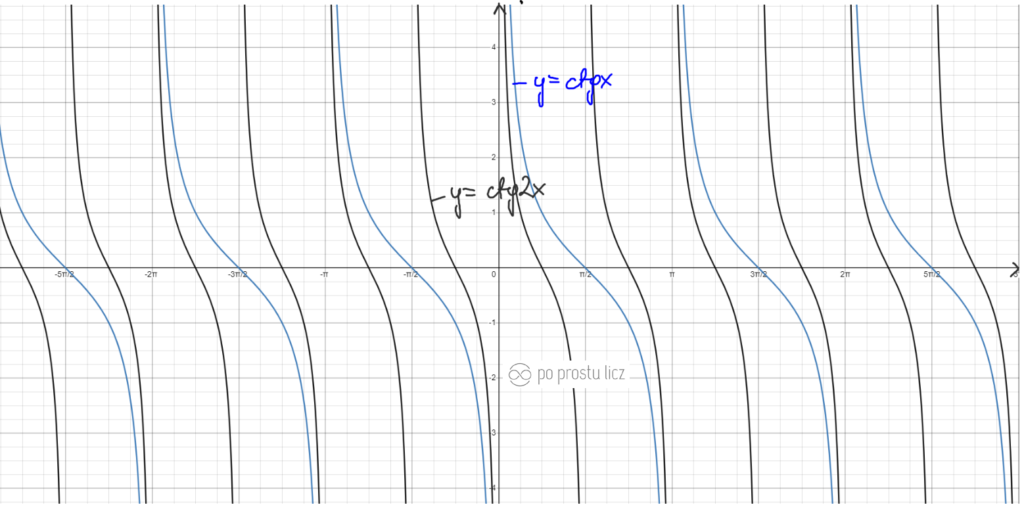
Wykres funkcji f(x)=14ctgx oraz f(x)=1/14ctgx.

• Niebieski to f(x)=ctgx.
• Czarny to f(x)=14ctgx.
• Czerwony to f(x)=1/14ctgx.

Przekształcenie funkcji f(ax) sinax, cosax, tgx, ctgax.

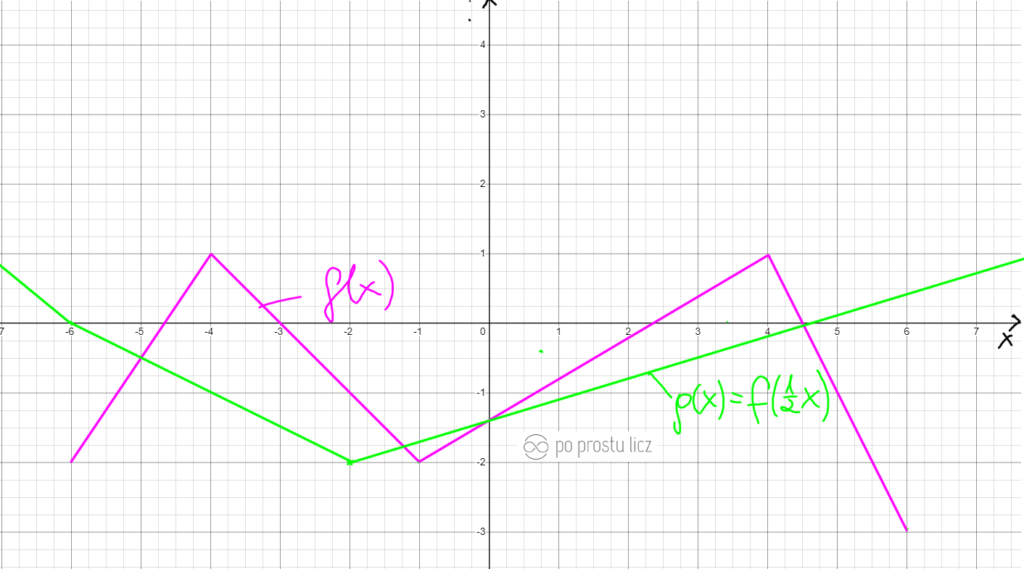
Szybkie przypomnienie o tym co to jest za przekształcenie g(x)=f(ax). Aby z wykresu f(x) otrzymać g(x) dany wykres albo rozciągnąć albo zwęzić. Wszystko robimy „po osi x”, wartości na osi y nie ruszamy. Spójrz na przykład.

Gdy liczba a jest z przedziału od 0 do 1.

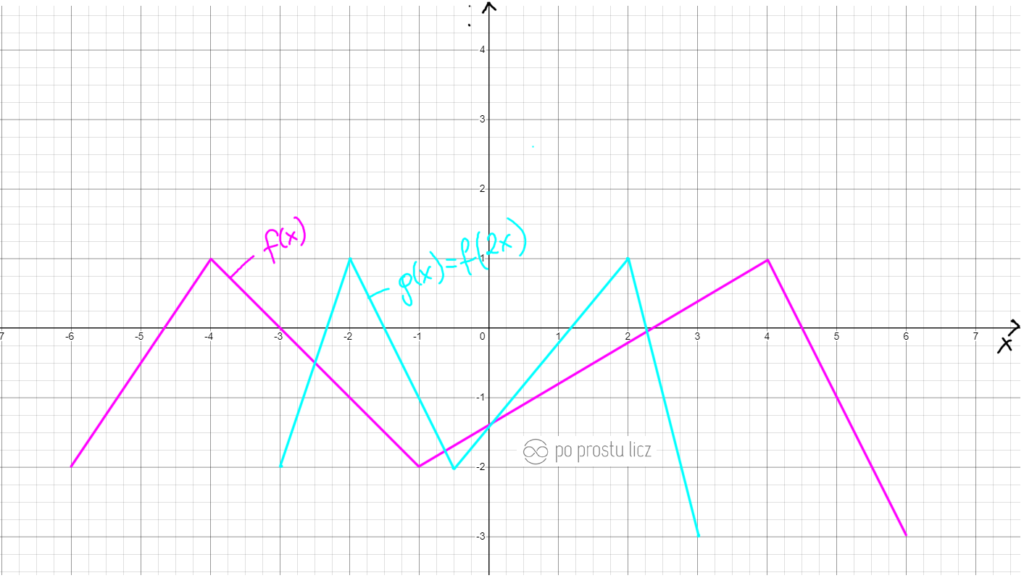
A gdy liczba a jest większa od 1, to robimy tak:

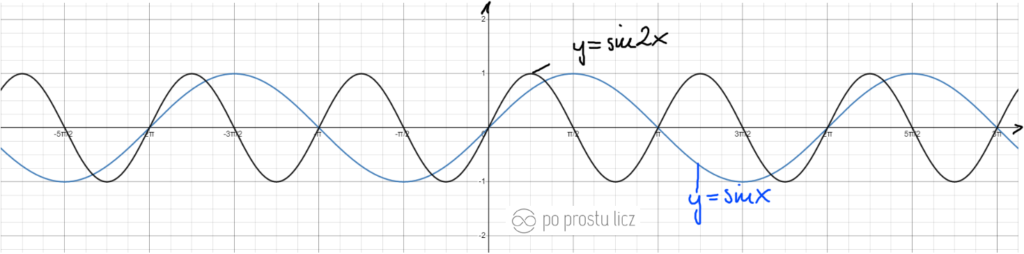
Wykres funkcji f(x)=sin2x oraz f(x)=sin1/2x.

• Niebieski to f(x)=sinx.
• Czarny to f(x)=sin2x.
• Czerwony to f(x)=sin1/2x.

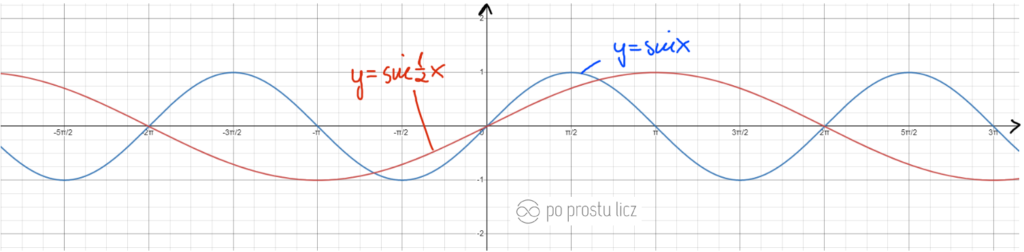
Zobacz film dotyczący przekształceń funkcji sinus i cosinus. Wykresy i przekształcenia wykresu funkcji trygonometrycznych zamieszam w tym filmy, to znaczy hop siup w Youtube klik.

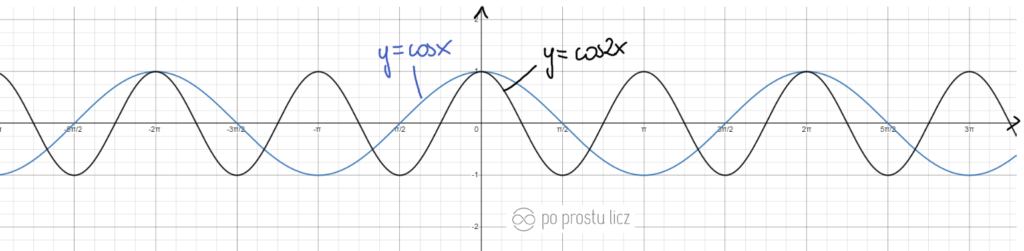
Wykres funkcji f(x)=cos4x oraz f(x)=cos1/4x.

• Niebieski to f(x)=cosx.
• Czarny to f(x)=cos4x.
• Czerwony to f(x)=cos1/4x.

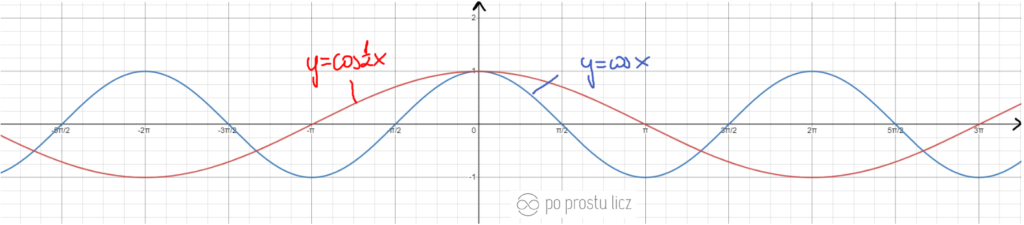
Lubisz słuchać jak opowiadam o wykresach? Albo jesteś ciekawa/ciekawy to SKOK W YOUTUBE.

Wykres funkcji f(x)=tg8x oraz f(x)=tg1/8x.

• Niebieski to f(x)=tgx.
• Czarny to f(x)=tg8x. – im większa liczba przed tangensem tym bardziej wykres przypomina prostą kreskę
• Czerwony to f(x)=tg1/8x. im większa liczba w mianowniku tym większą półkę ma tangens 😀 zerknij w film poniżej tam pokazuję dokładnie co i jak.

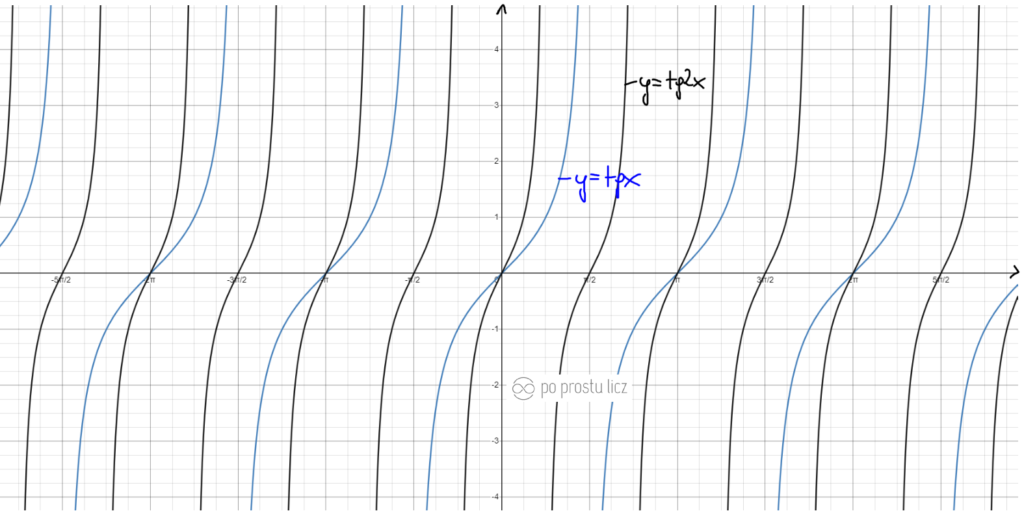
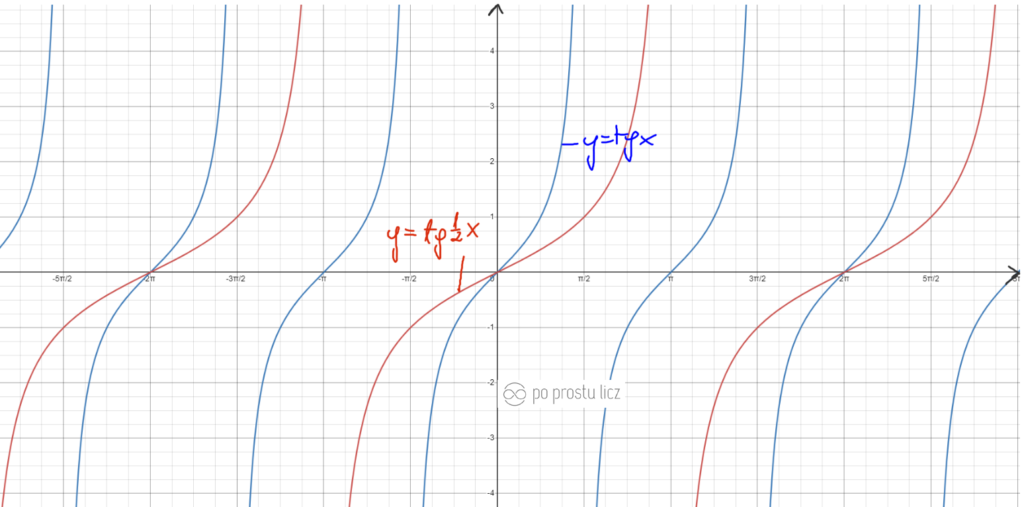
Wolisz posłuchać i zobaczyć więcej przykładów związanych z tymi przekształceniami zapraszam do poniższego filmu. Dokładnie tego o tutaj KLIK.

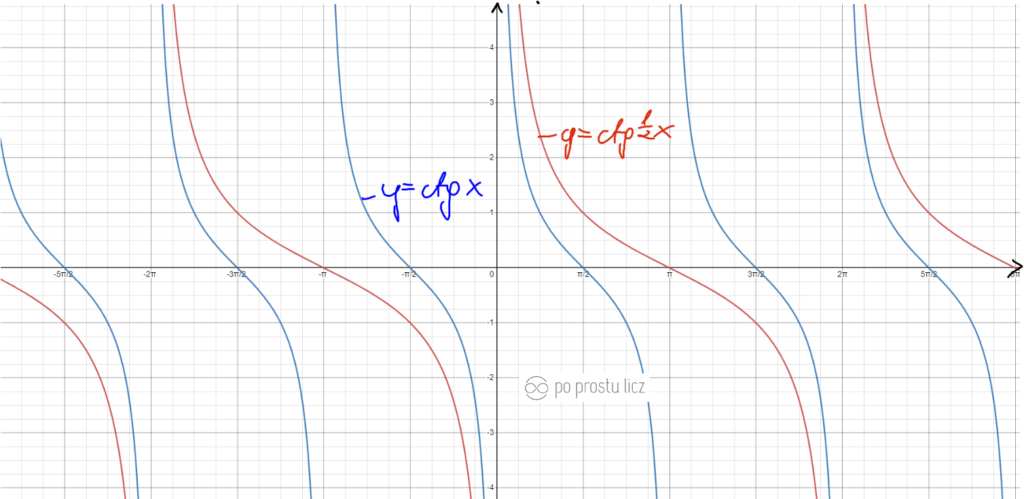
Wykres funkcji f(x)=ctg8x oraz f(x)=ctg1/8x.

• Niebieski to f(x)=ctgx.
• Czarny to f(x)=ctg8x.
• Czerwony to f(x)=ctg1/8x.

Uzupełnienie tematu albo po prostu warto tam zajrzeć:

• Przekształcenia wykresu do poczytania.PRZECHODZĘ.
• Lub jeśli wolisz słuchać o przekształceniach wykresu chodź na youtube. PRZECHODZĘ.