Wykres funkcji można przekształcić na kilka sposobów. W liceum ( lub technikum) w pierwszej klasie spotykasz taki temat przekształcanie wykresu funkcji i w tym dziale poznasz takie tematy jak:
- g(x)=(x)+q przesuwanie wykresu wzdłuż osi OY o q jednostek do góry lub w dół – przekształcenie wykresu funkcji wzdłuż osi OY CZYTAJ WIĘCEJ,
- g(x)=(x-p) przesuwanie wykresu wzdłuż osi OX o p jednostek w prawo lub w lewo – przekształcenie wykresu funkcji wzdłuż osi OX CZYTAJ WIĘCEJ,
- g(x)=(x-p)+q – przesuwanie wykresu o wektor [p,q], inaczej mówiąc translacja o wektor CZYTAJ WIĘCEJ,
- f(-x), -f(x) – przekształcenie wykresu przez symetrię względem osi układu współrzędnych CZYTAJ WIĘCEJ,
- |f(x)|, f(|x|) – inne przekształcenia wykresu, takie jak wartość bezwzględna CZYTAJ WIĘCEJ.
No to zaczynamy.
Przesuwanie (przekształcenie) wykresu wzdłuż osi OY
g(x)=f(x)+q lub g(x)=f(x)-q
Przesuwając wykres wzdłuż osi OY mamy tylko dwie możliwości: albo w górę, albo w dół. Poniżej rozpiszę na dwóch przykładach jak to wygląda. Zachęcam Ciebie do obejrzenia dodatkowych materiałów, bardziej szkolnych, sprawdzianowych ;),a teraz przed Tobą wprowadzenie do tematu.
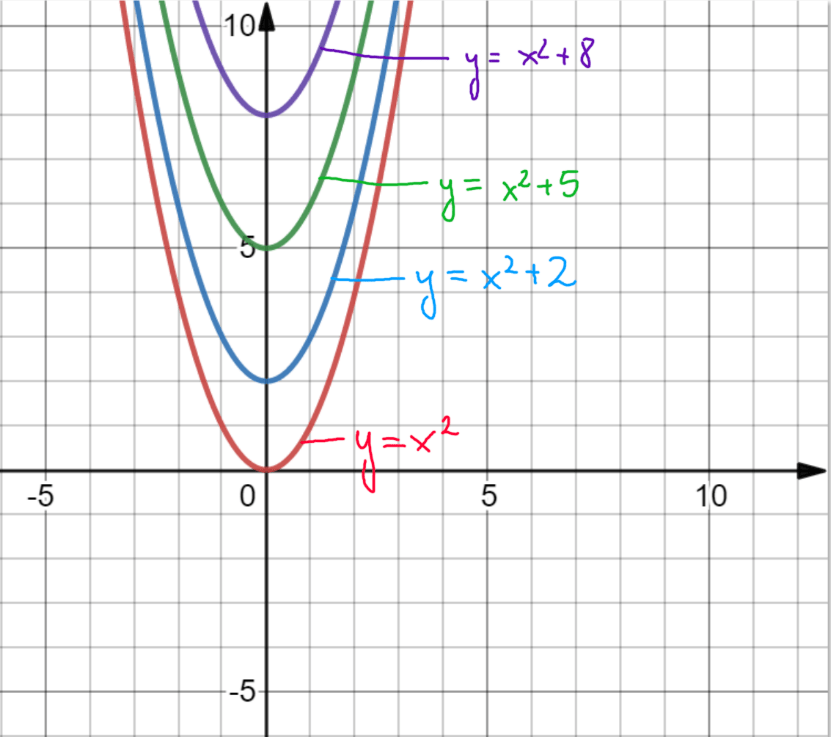
Wykres g(x)=f(x)+q dla q>0 otrzymujemy przez przesunięcie wykresu y=f(x) o q jednostek w górę wzdłuż osi OY.
Funkcje, które są na wykresie to:
- wyk1. y=x2
- wyk2. y=x2 + 2
- wyk3. y=x2 + 5
- wyk4. y=x2 + 8
Te liczby, które zaznaczyłam na pomarańczowo to nasze q z tego wzoru g(x)=f(x)+q.
Spójrz na poniższy wykres lub wzory powyżej. Widzisz, za każdym x2 jest + i jakaś liczba, i to dzięki temu, wiem, że wykres muszę przesunąć do góry.
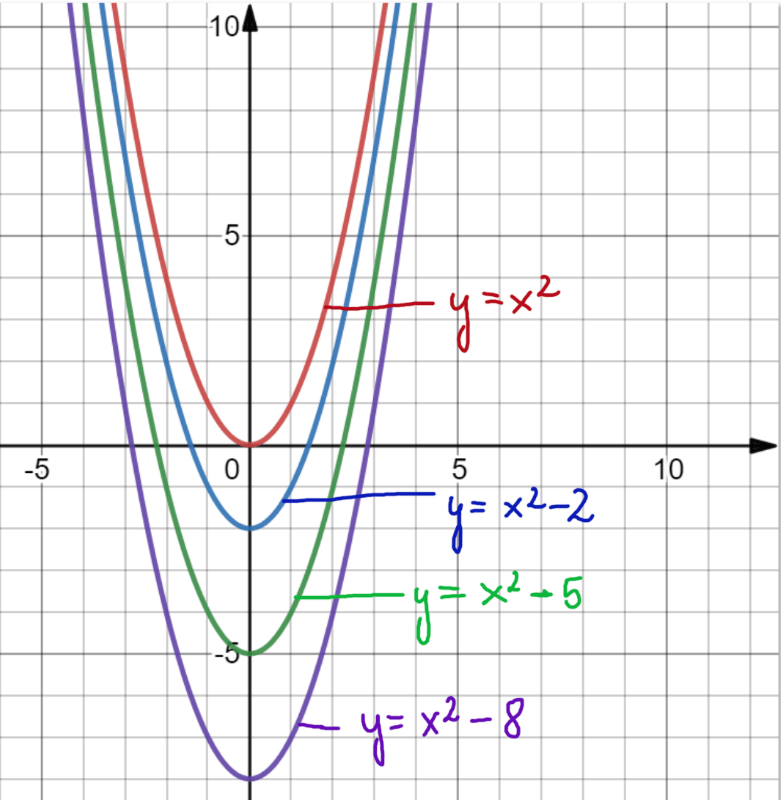
Wykres g(x)=f(x)-q dla q>0 otrzymujemy przez przesunięcie wykresu y=f(x) o q jednostek w dół wzdłuż osi OY.
Funkcje, które są na wykresie to:
- wyk1. y=x2
- wyk2. y=x2 – 2
- wyk3. y=x2 – 5
- wyk4. y=x2 – 8
Te liczby, które zaznaczyłam na pomarańczowo to nasze q z tego wzoru g(x)=f(x) – q.
I tutaj też spójrz na wzory funkcji, która mamy na wykresie. Za każdym naszym x2 jest –, i właśnie to, że ten minus jest za x2, mówi nam o tym, że wykres przesuwamy w dół.
Podsumowując:
Przekształcanie wykresu funkcji wzdłuż osi OY rozpoznaję po tym, że gdzieś x mam +/- jakąś liczbę. Lepiej spójrz poniżej. (Nie martw się, zaraz zobaczysz jak odróżnić to od przesuwania względem osi OX).
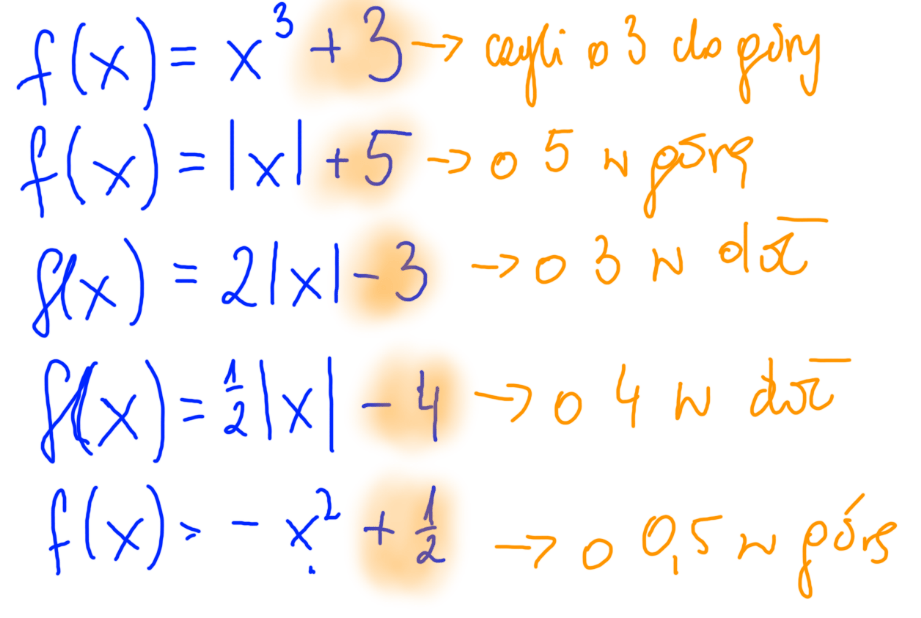
I kolejny przykład na podsumowanie, tym razem z wartością bezwzględną, byś mógł drogi uczniu zobaczyć jeszcze więcej przykładów.
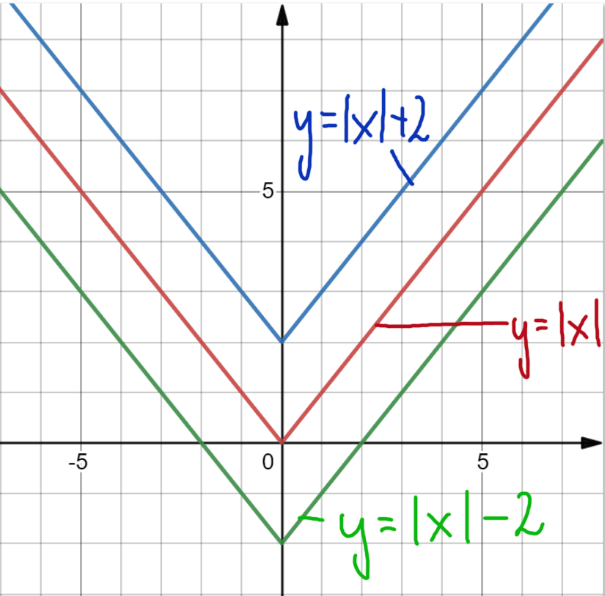
Przesuwanie (przekształcenie) wykresu wzdłuż osi OX
g(x)=f(x+q) lub g(x)=f(x-q)
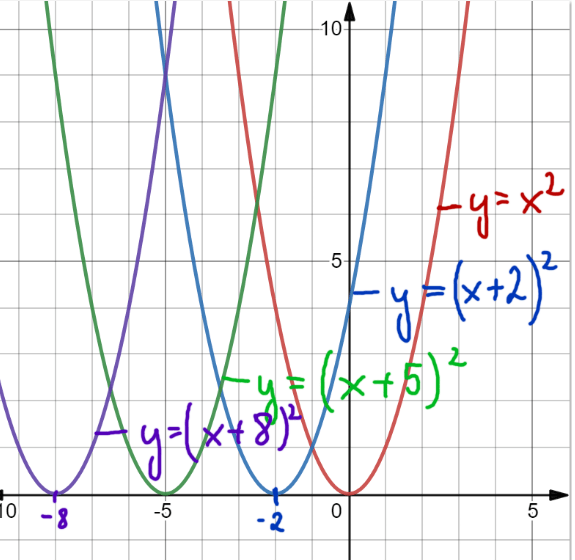
Wykres g(x)=f(x+p) dla p>0 otrzymujemy przez przesunięcie wykresu y=f(x) o p jednostek w LEWO wzdłuż osi OX.
Funkcje, które są na wykresie to:
- wyk1. y=x2
- wyk2. y=(x + 2)2
- wyk3. y=(x + 5)2
- wyk4. y=(x + 8)2
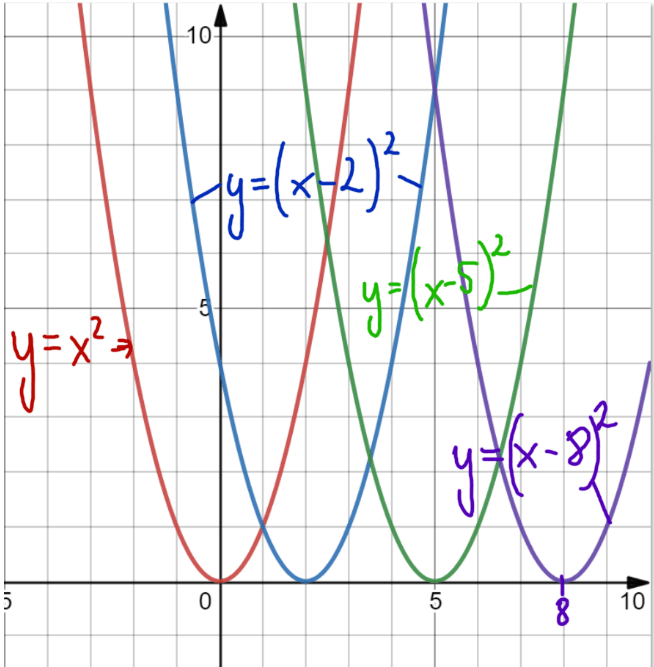
Wykres g(x)=f(x-p) dla p>0 otrzymujemy przez przesunięcie wykresu y=f(x) o p jednostek w PRAWO wzdłuż osi OX.
Funkcje, które są na wykresie to:
- wyk1. y=x2
- wyk2. y=(x – 2)2
- wyk3. y=(x – 5)2
- wyk4. y=(x – 8)2
Podsumowując:
Przekształcanie wykresu funkcji wzdłuż osi OX rozpoznaję po tym, że zaraz bliziutko mojego x mam liczbę. Brzmi hard corowo, ale ale spójrz poniżej na przykłady.
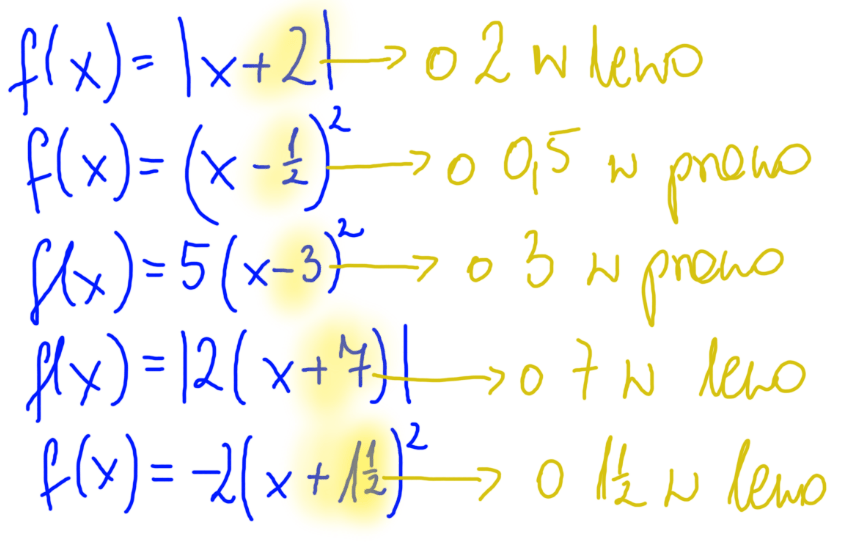
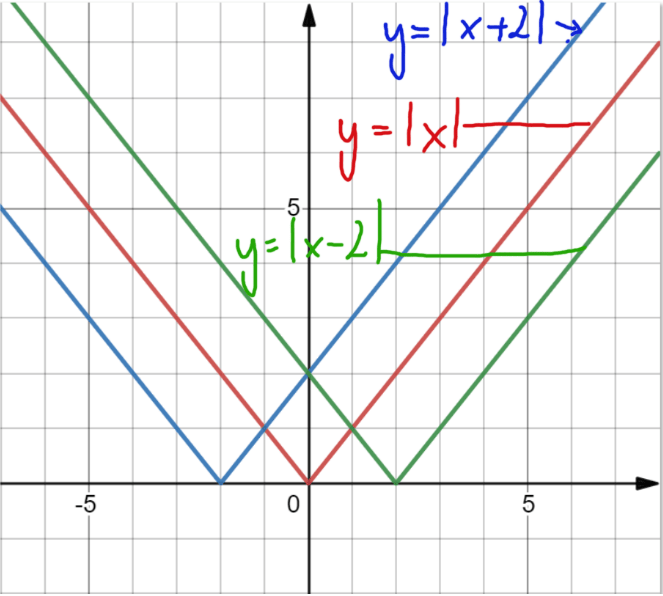
I jeszcze przykład z wartością bezwzględną. Tak dla pewności.
Przesuwanie wykresu o wektor [p,q], inaczej mówiąc translacja o wektor g(x)=(x-p)+q
Przesunięcie wykresu o wektor [p, q] polega na przesunięciu wykresu w poziomie o p i w pionie o q.
Zróbmy od razu konkretny przykład.
Przesuń wykres funkcji y=|x| o wektor:
- [1,5]
- [-1,2]
- [1,-2]
- [-3,-4]
- [0,3]
- [3,0]
By przesunąć wykres funkcji y=|x| o podany wektor, zaczynamy od narysowania wykresu funkcji y=|x|.
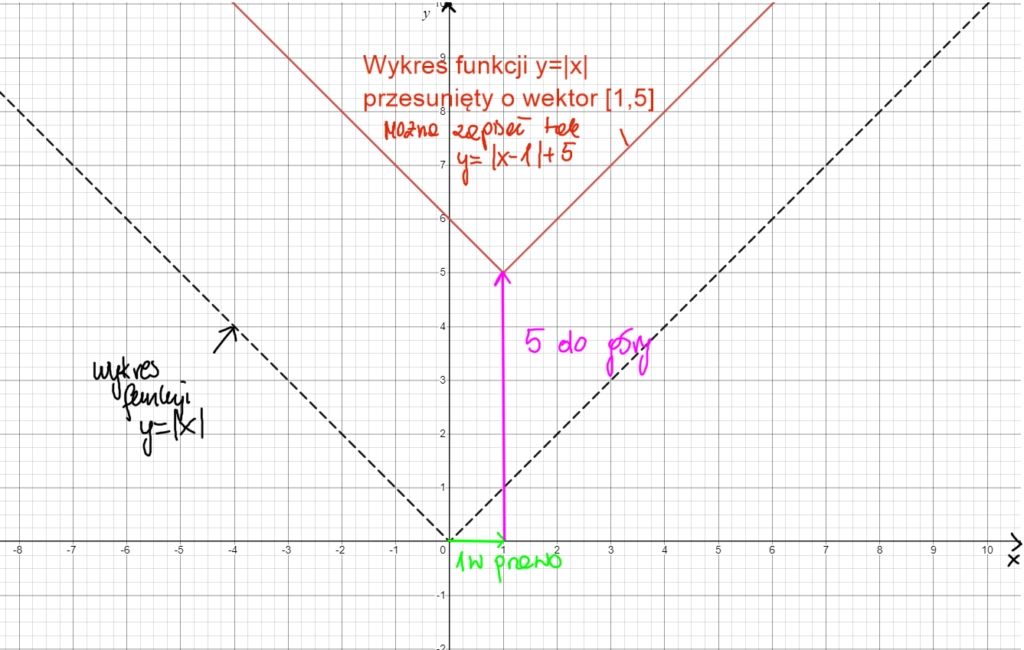
Przesunięcie wykresu y=|x| o wektor [1,5]. Przesuwamy wykres w poziomie o 1 (w prawo) i w pionie o 5 ( 5 do góry).
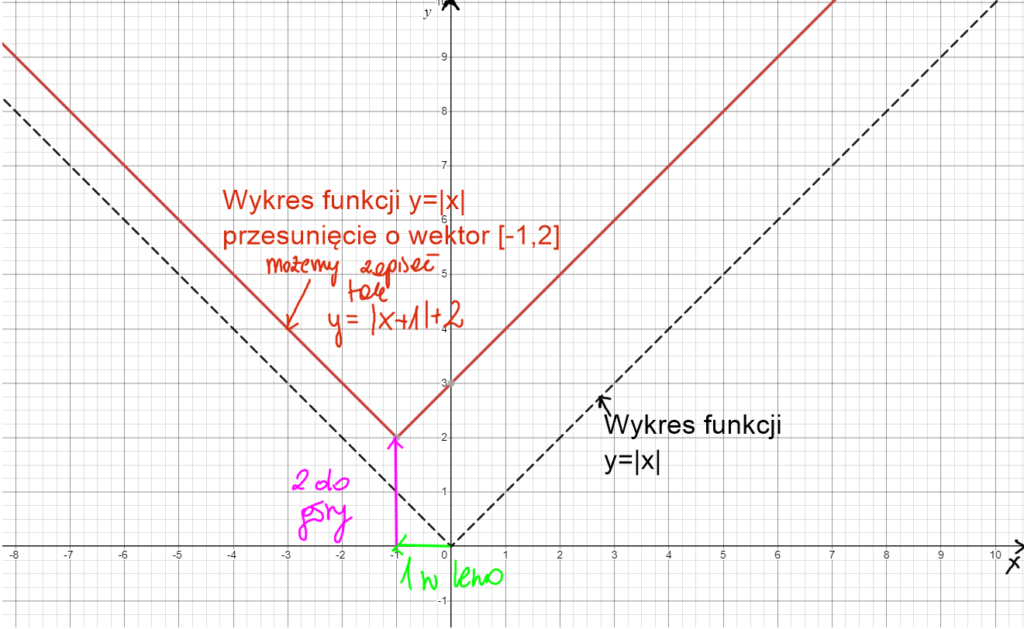
Przesunięcie wykresu y=|x| o wektor [-1,2]. Przesuwamy wykres w poziomie o 1 (w lewo) i w pionie o 2 ( 2 do góry).
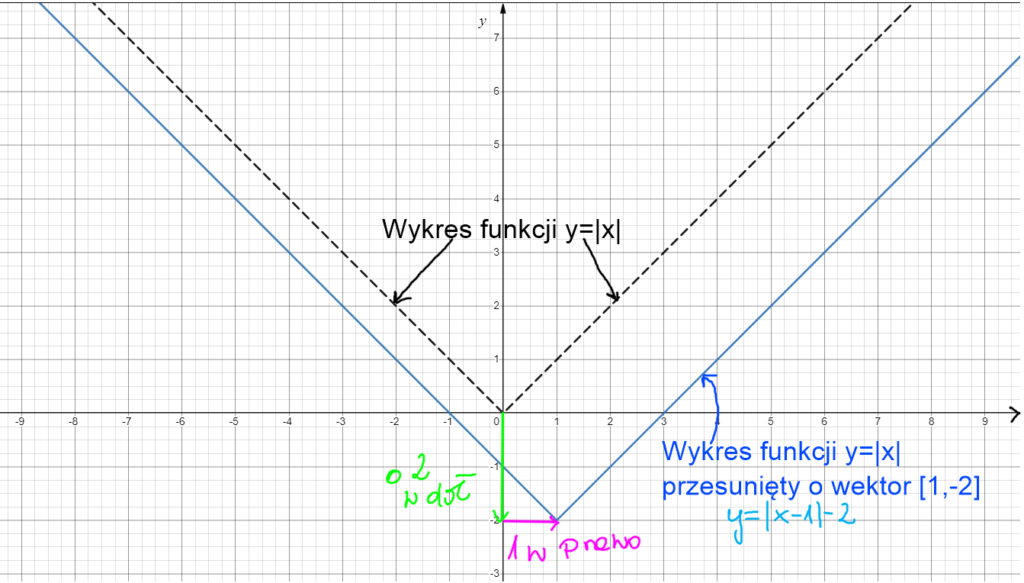
Przesunięcie wykresu y=|x| o wektor [1,-2]. Przesuwamy wykres w poziomie o 1 (w prawo) i w pionie o -2 ( -2 w dół).
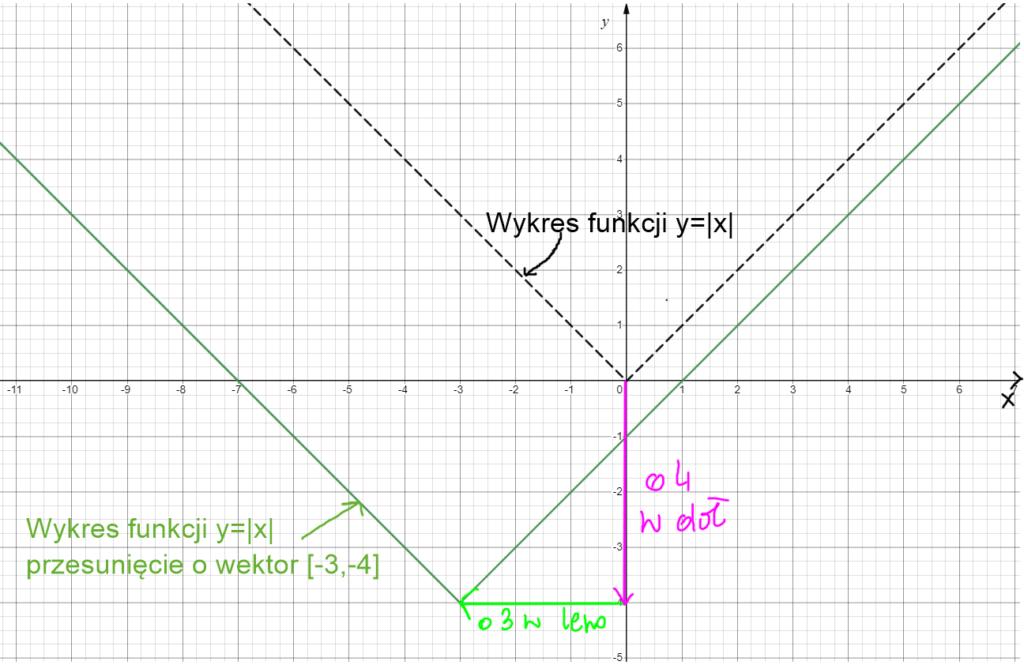
Przesunięcie wykresu y=|x| o wektor [-3,-4]. Przesuwamy wykres w poziomie o 3 (w lewo) i w pionie o -4 ( -4 w dół).
Przesunięcie wykresu y=|x| o wektor [0,-3]. Przesuwamy wykres w poziomie o 0 ( nie przesuwamy w lewo ani w prawo) i w pionie o 3 ( 3 w dół).
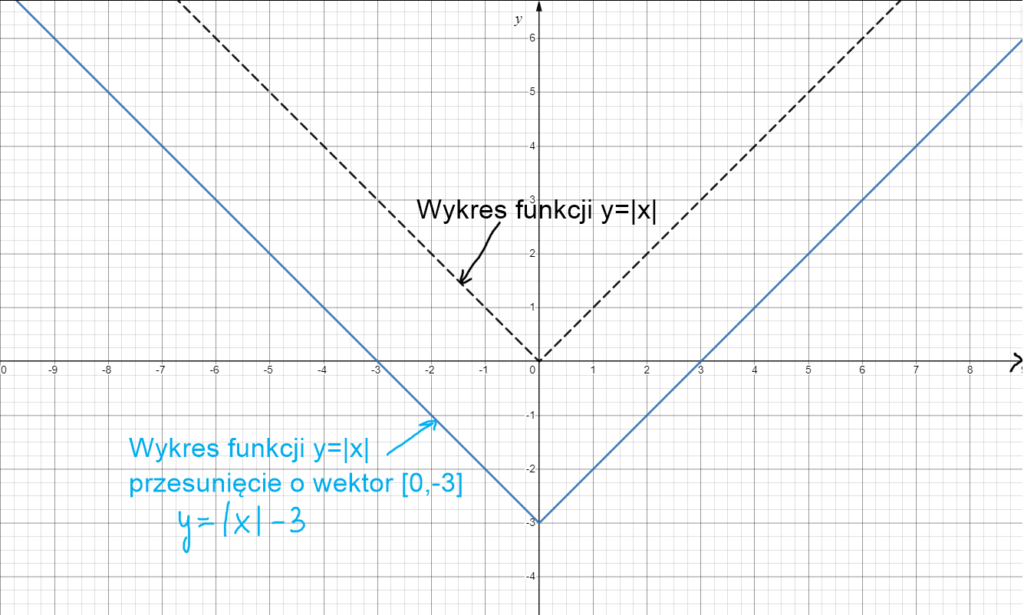
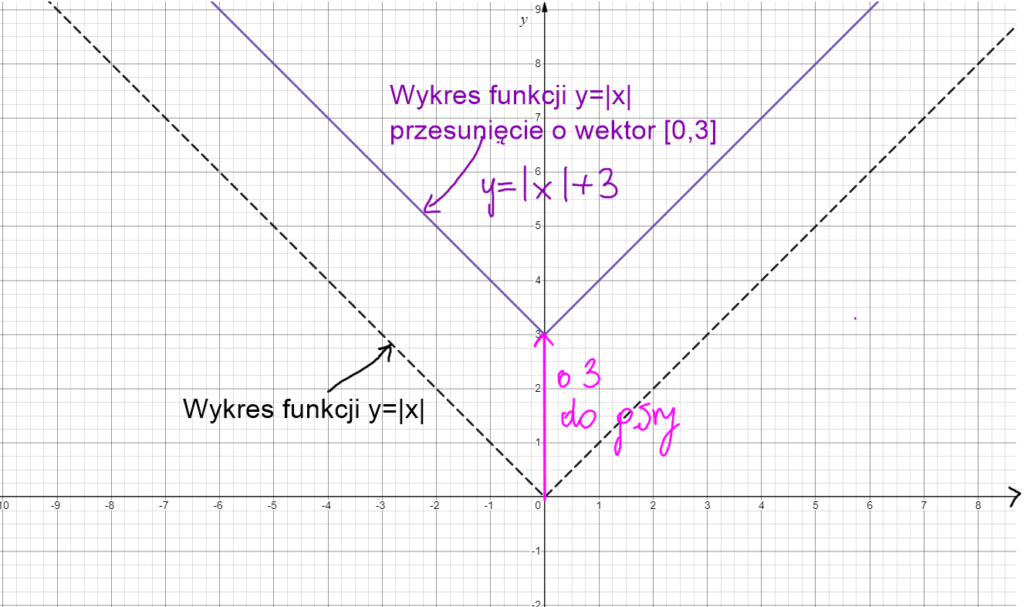
Przesunięcie wykresu y=|x| o wektor [0,3]. Przesuwamy wykres w poziomie o 0 (hihihi czyli nie przesuwamy w lewo ani w prawo) i w pionie o 3 ( 3 w górę).
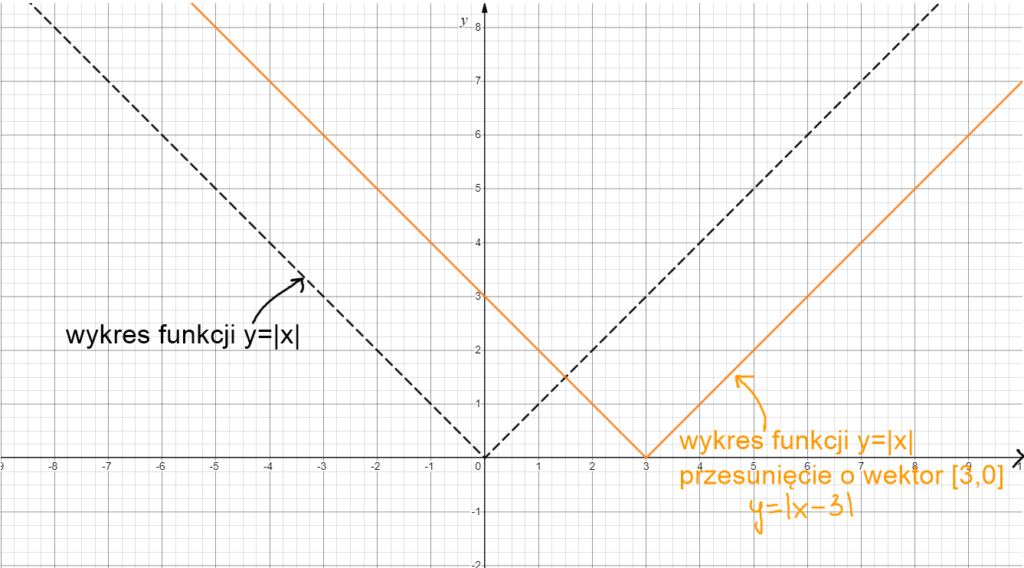
Przesunięcie wykresu y=|x| o wektor [3,0]. Przesuwamy wykres w poziomie o 3 ( w prawo ) i w pionie o 0 ( hehe czyli nie przesuwamy go w górę ani dół).
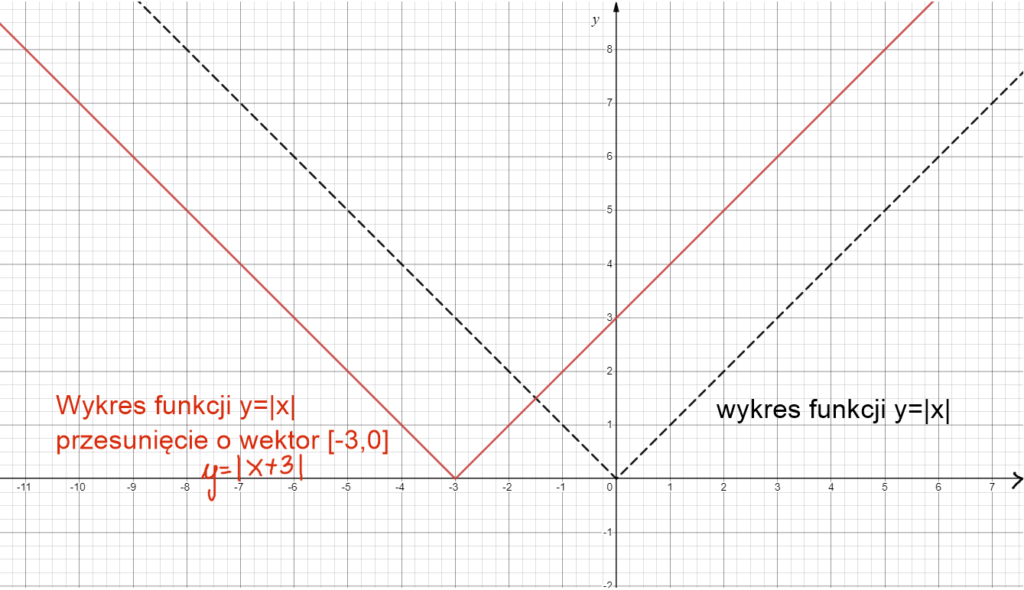
Przesunięcie wykresu y=|x| o wektor [-3,0]. Przesuwamy wykres w poziomie (oś OX) o 3 ( w lewo ) i w pionie o 0 ( czyli nie przesuwamy go w górę ani dół).
Podsumowanie a raczej uzupełnienie tematu o przesuwaniu funkcji o wekor.
Funkcja f(-x) jest przykładem przekształcenia symetrycznego względem osi x. Oznacza to, że każdy punkt o współrzędnych (x,y) na wykresie funkcji f(x) zostanie zamieniony na punkt o współrzędnych (-x,y) na wykresie funkcji f(-x). Efektem takiego przekształcenia będzie lustrzane odbicie wykresu funkcji f(x) względem osi x.
Natomiast funkcja -f(x) jest przykładem przekształcenia symetrycznego względem osi y. Oznacza to, że każdy punkt o współrzędnych (x,y) na wykresie funkcji f(x) zostanie zamieniony na punkt o współrzędnych (x,-y) na wykresie funkcji -f(x). Efektem takiego przekształcenia będzie lustrzane odbicie wykresu funkcji f(x) względem osi y.
Ten temat będę na bieżąco rozszerzać o kolejne przekształcenia.








