Dzisiaj kontynuuję naszą podróż przez zagadnienia szeregów rozdzielczych, z głównym naciskiem na analizę struktury takiego szeregu. Nasz główny punkt zainteresowania to ’Średnia arytmetyczna dla szeregu rozdzielczego’, stanowiąca jedną z najważniejszych miar położenia w statystyce.
Średnia arytmetyczna, zwłaszcza w kontekście szeregu rozdzielczego, może być obliczana na wiele różnych sposobów. Ta różnorodność pozwala na użycie różnych wzorów i metod, co sprawia, że niezależnie od Twojego poziomu zaawansowania, na pewno znajdziesz tu coś, co przyciągnie Twoją uwagę. W dalszej części tego wpisu przedstawię kilka tych wzorów, które są stosowane do obliczania 'Średniej arytmetycznej dla szeregu rozdzielczego’, zaopatrując je w praktyczne przykłady obliczeń.
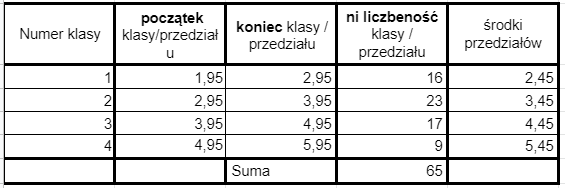
Przykład, który będę używać, oparty jest na danych pochodzących z mojego poprzedniego wpisu (aby do niego wrócić, kliknij tutaj), który dotyczył szeregu rozdzielczego. W tym momencie nie będę więc tworzyć nowego szeregu rozdzielczego, lecz skorzystam z istniejących już danych. Dla wygody, ponownie prezentuję te dane poniżej, aby ułatwić Ci śledzenie moich obliczeń dotyczących 'Średniej arytmetycznej dla szeregu rozdzielczego’.
Zadanie – policz średnią dla szeregu rozdzielczego.
Zebrano dane dotyczące wyników egzaminu ze statystyki pewnej grupy studentów na kierunku marketing.
Otrzymano następujące dane:
2, 2, 3, 4, 5, 5, 2, 3, 4, 5, 3, 4, 5, 2, 3, 3, 5, 3, 3, 3, 2, 3, 4, 2, 2, 3, 4, 3, 2, 3, 2, 3, 3, 2, 4, 5, 3, 2, 2, 3, 4, 3, 3, 4, 2, 2, 5, 3, 3, 2, 4, 5, 3, 3, 2, 4, 4, 4, 5, 3,4, 4, 4,4, 4.
Utworzyć szereg rozdzielczy szczegółowy dla podanych danych, a następnie przeprowadzić analizę struktury wyników z egzaminu (określić wartość średnią, odchylenie standardowe, modę, medianę, współczynnik zmienności i typowy obszar zmienności, sporządzić histogram). Przekreślonym się na razie nie przejmujemy.
Zanim jednak przejdziemy do szczegółowych obliczeń, warto zrozumieć, jak obliczyć średnią w szeregu rozdzielczym. Najpierw wyznaczymy szereg rozdzielczy dla naszego przykładu, a następnie skupimy się na wyjaśnieniu wzoru na średnią arytmetyczną w szeregu rozdzielczym.
Jak obliczyć średnią w szeregu rozdzielczym?
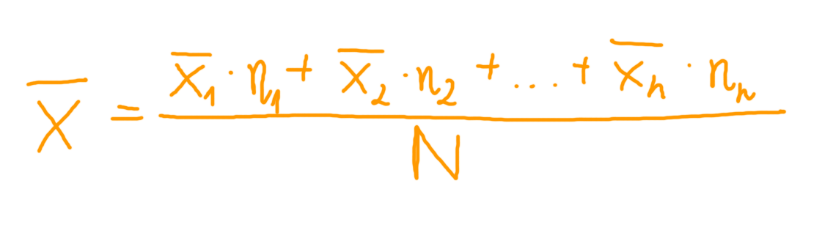
Wzór na obliczenie średniej arytmetycznej dla szeregu rozdzielczego: prosty przewodnik dla studentów
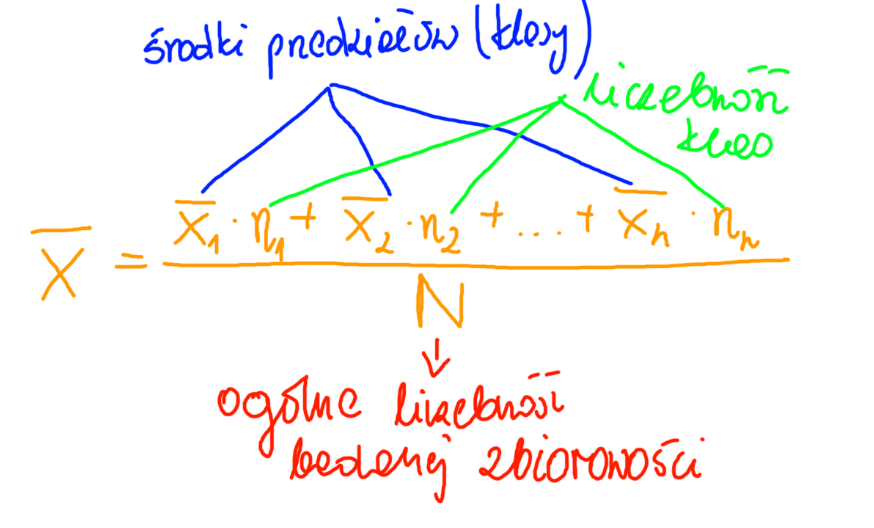
Cieszę się, że mogę podzielić się z Tobą analizą tego, co dokładnie oznacza każdy element we wzorze na średnią arytmetyczną dla szeregu rozdzielczego. Na przykładzie przedstawionym na załączonym obrazku zobaczysz trzy kluczowe komponenty: środki przedziałów klasy, liczebność klasy oraz ogólną liczebność badanej zbiorowości.
- Środki przedziałów klasy (xᵢ): To są punkty centralne przedziałów klasy, które wyznaczamy dla każdego przedziału klasy w naszym szeregu rozdzielczym. Są one zwykle obliczane jako średnia z górnej i dolnej granicy danego przedziału klasy.
- Liczebność klasy (nᵢ): Liczebność klasy odnosi się do liczby elementów (obserwacji) w danym przedziale klasy. Mówi nam, ile razy dany przedział występuje w naszej badanej zbiorowości.
- Ogólna liczebność badanej zbiorowości (N): Jest to suma wszystkich obserwacji w szeregu rozdzielczym. W praktyce jest to suma liczebności wszystkich klas.
Średnia arytmetyczna dla szeregu rozdzielczego obliczana jest za pomocą następującego wzoru:
Średnia = (Σ (xᵢ * nᵢ)) / N
Gdzie:
- Σ oznacza sumę wartości dla wszystkich klas
- xᵢ * nᵢ to iloczyn środka przedziału klasy (xᵢ) oraz liczebności klasy (nᵢ)
- N to ogólna liczebność badanej zbiorowości.
Kiedy już zrozumiesz, co oznacza każdy z tych elementów, obliczanie średniej arytmetycznej dla szeregu rozdzielczego staje się znacznie łatwiejsze!
Średnia arytmetyczna dla szeregu rozdzielczego w naszym przykładzie.
Obliczenie średniej arytmetycznej dla szeregu rozdzielczego wymaga pomnożenia środków naszych przedziałów lub klas przez ich liczebność, co reprezentowane jest w ostatniej kolumnie naszych danych. Mówiąc inaczej musimy pomnożyć środki naszych przedziałów / klas przez ich liczebność (ostatnia kolumna).
Ale jeśli chcesz zrozumieć więcej, to już śpieszę z wyjaśnieniem.
Obliczenie średniej arytmetycznej dla szeregu rozdzielczego to proces, który może początkowo wydawać się nieco skomplikowany, ale z pewnością jest do opanowania. Proces ten obejmuje wykonanie pewnych specyficznych obliczeń, które związane są z danymi zawartymi w naszym szeregu.
Kluczowym krokiem jest pomnożenie środków naszych przedziałów lub klas (które są pewnego rodzaju „średnią” dla każdego przedziału) przez ich liczebność, czyli ilość elementów, które się w nich znajdują. To działanie reprezentowane jest w ostatniej kolumnie naszych danych. Oznacza to, że musimy wykonać operację mnożenia dla każdego z naszych przedziałów lub klas.
Dlaczego to robimy?
Ponieważ to nam pozwala uzyskać bardziej precyzyjny obraz naszych danych. Zamiast po prostu średniej arytmetycznej wszystkich danych, możemy uzyskać średnią arytmetyczną dla każdego przedziału lub klasy, która uwzględnia liczebność tych przedziałów lub klas. W ten sposób zyskujemy bardziej szczegółowy obraz naszych danych, który może być niezwykle wartościowy w wielu kontekstach badawczych.
To działanie wykonujemy dla każdego z przedziałów lub klas, a następnie sumujemy wyniki. Wynik ten dzielimy przez ogólną liczebność badanej zbiorowości, czyli całkowitą liczbę elementów w naszym szeregu rozdzielczym.
Poniżej znajduje się tabela, w której przedstawiam krok po kroku, jak dokładnie przeprowadzić to obliczenie. Czytając tę tabelę, zrozumiesz, jakie kroki są konieczne do obliczenia średniej arytmetycznej dla szeregu rozdzielczego i zobaczysz, jak te kroki są reprezentowane w praktyce.
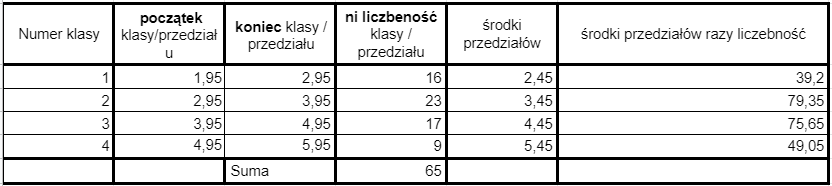
Teraz wszystko co mamy podstawiam do wzoru.
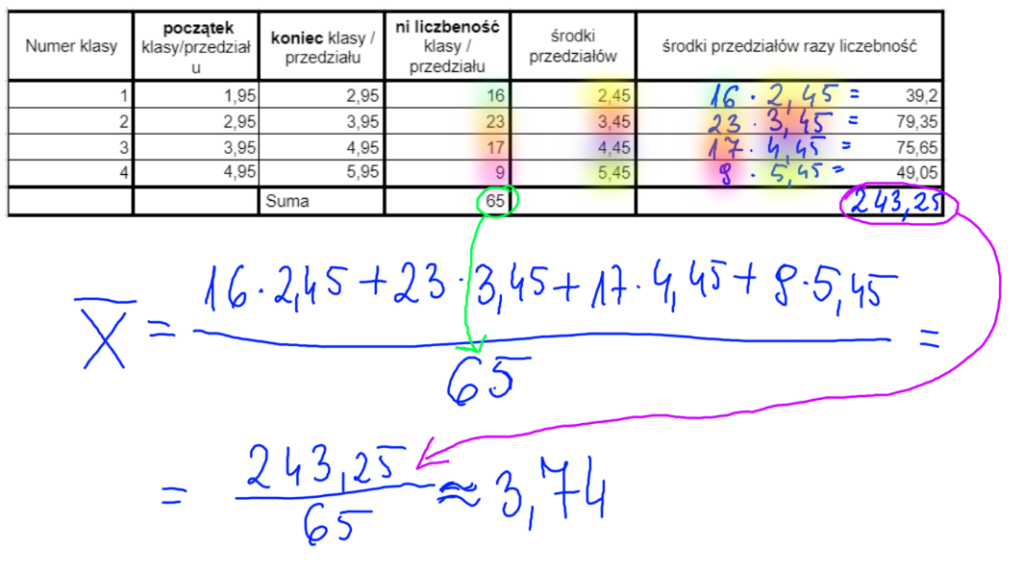
Gotowi na trochę magii matematycznej?
Właśnie wzięliśmy na warsztat obliczanie średniej arytmetycznej dla szeregu rozdzielczego i wygląda to naprawdę fajnie. Chodzi tu o szaloną zabawę z mnożeniem środków naszych przedziałów klas przez ich liczebność. W praktyce oznacza to, że bierzemy te środki, mnożymy je przez liczbę razy, ile się pojawiają, a potem dodajemy to wszystko razem. To wszystko wrzucamy do magicznego matematycznego kotła, który nazywamy „wzorem”.
I co z tego wyszło? Jaki jest wynik średniej ?
Otóż, po dokonaniu tych matematycznych czarów, otrzymujemy wynik średniej arytmetycznej równy 3,74. To jest ta tajemnicza liczba, którą właśnie obliczyliśmy dla naszego szeregu rozdzielczego.
Ale nie oszukujmy się, matematyka to nie jest tylko jeden poprawny sposób rozwiązania problemu. To trochę jak z wejściem do labiryntu – jest wiele ścieżek, które prowadzą do mety! Więc zróbmy to jeszcze raz, tyle że tym razem użyjemy innego wzoru, bo przecież kto by nie chciał znać więcej niż jednego tricku, prawda?
Więc chodźcie, przygotujcie się na kolejną rundę matematycznej magii i zobaczmy, co stanie się, gdy użyjemy tego nowego wzoru!
Zrozumienie różnych dróg do jednego celu to właśnie jest sedno nauki matematyki.
Więc na co czekamy? Zróbmy to!
Średnia arytmetyczna dla szeregu rozdzielczego innym sposobem wykorzystując częstość
Pamiętaj, że w matematyce zawsze jest więcej niż jedna droga dojścia do rozwiązania. I zgodnie z tą filozofią, podejdziemy do średniej arytmetycznej dla szeregu rozdzielczego od zupełnie innej strony!
Czy jesteś gotów?
No dobrze, złap za długopis, bo dodajemy do naszej tabelki nową kolumnę – tym razem kolumnę z częstością.
Cóż to za zaskakujący zwrot akcji, prawda?
Co to jest częstość w szeregu rozdzielczym?
Możesz się zastanawiać, co to jest „częstość”.
Otóż, to jest wynik podzielenia liczebności danego przedziału przez sumę wszystkich wyników.
Wszystko jest tutaj o proporcje, moj drogi. Zrozumienie tego pomoże Ci w przyszłości, obiecuję!
Ale tutaj jest haczyk – suma wszystkich częstości musi wynosić 1.
Tak, słyszysz dobrze, dokładnie 1.
Jeśli Twoje obliczenia prowadzą Cię gdziekolwiek indziej… eh, coś poszło nie tak.
Wiem, wiem, wszyscy popełniamy błędy, ale trzeba na nie uważać.
Jeżeli dodasz wszystkie częstości i okaże się, że wynik jest większy niż 1, to jest to jak mówi ten stary żart – „Houston, mamy problem”.
Ale bez obaw, razem przejdziemy przez to krok po kroku. Więc bądź gotów na trochę matematycznej zabawy!
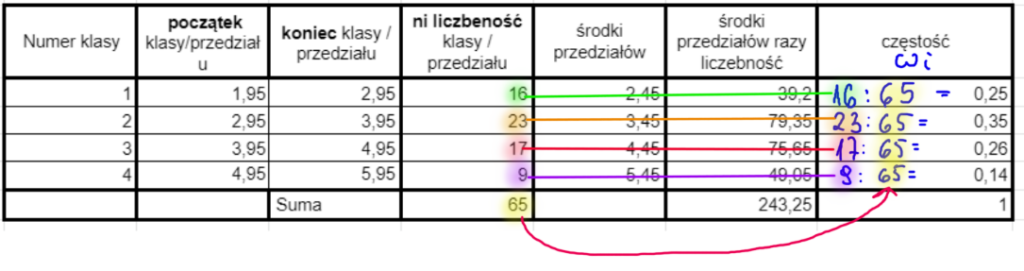
Obliczywszy częstości dla szeregu rozdzielczego, możemy skorzystać z kolejnego wzoru na średnią arytmetyczną w szeregu rozdzielczym, tym razem wykorzystując częstości. Dzięki temu obliczamy średnią arytmetyczną dla szeregu rozdzielczego na nowo, korzystając z częstości.
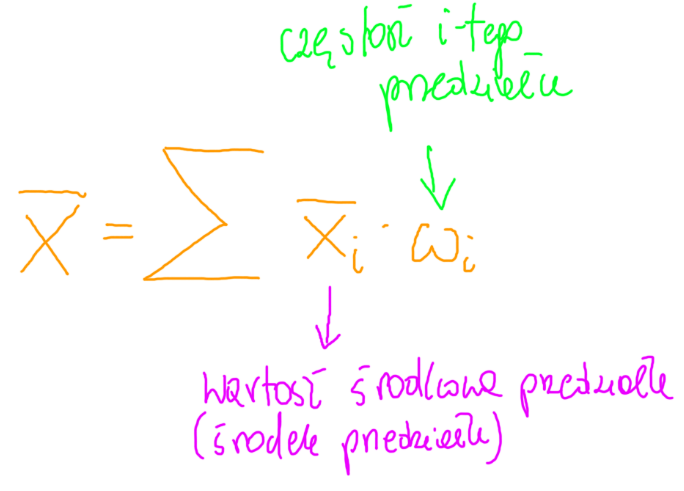
Zatem pomnożę środki przedziałów by móc skorzystać z powyższego wzoru na średnią dla szeregu rozdzielczego.
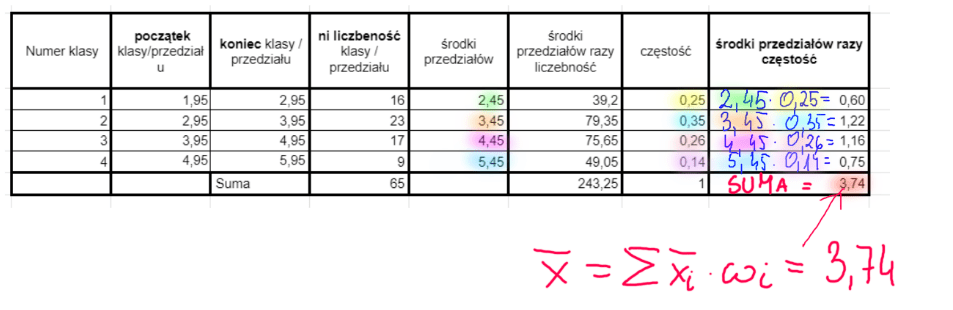
Średnia arytmetyczna dla szeregu rozdzielczego – interpretacja wyniku
Średnio uczeń otrzymał ocenę 3,74. I hmm co to znaczy, widzimy, że liczba 3,74 nie występuję w naszych danych. Nie ma takiej oceny.
Czy to znaczy, że wyszło nam coś źle?
Wszystko dobrze nam wyszło, wartość średniej arytmetycznej nie musi być równa jakiejkolwiek liczbie występującej w naszym zadaniu.
Tak naprawdę średnia nie mówi nam za wiele o tym jak liczby są rozłożone w naszej próbce.
Więc jak interpretować wynik średniej arytmetycznej dla szeregu rozdzielczego?
Średnio student otrzymał ocenę 3,74. Co to oznacza?
Widzimy, że liczba 3,74 nie występuje w naszych danych, a co za tym idzie, nie ma takiej oceny. Czy to oznacza, że coś poszło nie tak? Nie, wszystko jest w porządku. Wartość średniej arytmetycznej nie musi odpowiadać żadnej z liczb występujących w naszych danych.
W rzeczywistości, średnia sama w sobie nie mówi nam wiele o tym, jak liczby są rozłożone w naszej próbce. Jest to jedynie wartość, która pozwala nam na uproszczone spojrzenie na nasze dane. Aby zdobyć pełniejsze i bardziej szczegółowe informacje na temat naszego szeregu, musimy zanalizować takie parametry jak wariancja i odchylenie standardowe. Ale o tym opowiemy już w kolejnym artykule.
Kolejna część to wariancja i odchylenie standardowe.


