Statystyka opisowa na studiach często zaczyna się od tego zagadnienia czyli od szeregu rozdzielczego. Szereg rozdzielczy pomaga nam zapanować nad dużą ilością danych. Dzięki niemu nasza próbka wygląda ładniej dla oka. Niestety w szeregu rozdzielczym trochę inaczej liczmy średnią arytmetyczną, medianę itd., ale o tym w innym wpisie. Dziś będziemy uczyć się jak stworzyć szereg rozdzielczy. Od razu mam dla nas jedno zadanie, które będziemy wykorzystywać i na jego przykładzie tworzyć szereg rozdzielczy.

Zadanie – zrób szereg rozdzielczy.

Zebrano dane dotyczące wyników egzaminu ze statystyki pewnej grupy studentów na kierunku marketing.

Otrzymano następujące dane:

2, 2, 3, 4, 5, 5, 2, 3, 4, 5, 3, 4, 5, 2, 3, 3, 5, 3, 3, 3, 2, 3, 4, 2, 2, 3, 4, 3, 2, 3, 2, 3, 3, 2, 4, 5, 3, 2, 2, 3, 4, 3, 3, 4, 2, 2, 5, 3, 3, 2, 4, 5, 3, 3, 2, 4, 4, 4, 5, 3,4, 4, 4,4, 4.

Utworzyć szereg rozdzielczy szczegółowy dla podanych danych, a następnie przeprowadzić analizę struktury wyników z egzaminu (określić wartość średnią, odchylenie standardowe, modę, medianę, współczynnik zmienności i typowy obszar zmienności, sporządzić histogram). Przekreślonym się na razie nie przejmujemy.

Od czego zacząć gdy tworzymy szereg rozdzielczy?

Od zrobienia porządku. Układamy nasze liczby od najmniejszej do największej.

Mam podane liczby tak:

2, 2, 3, 4, 5, 5, 2, 3, 4, 5, 3, 4, 5, 2, 3, 3, 5, 3, 3, 3, 2, 3, 4, 2, 2, 3, 4, 3, 2, 3, 2, 3, 3, 2, 4, 5, 3, 2, 2, 3, 4, 3, 3, 4, 2, 2, 5, 3, 3, 2, 4, 5, 3, 3, 2, 4, 4, 4, 5, 3,4, 4, 4,4, 4.

W kolejności rosnącej wygląda tak:

2  2  2  2  2  2  2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5

Liczymy ile mamy wyników:

Mamy 65 oceń.

czyli n=65.

Jak obliczyć rozstęp badanej cechy?

Właśnie po to robiliśmy porządek z naszymi danymi i układaliśmy je w kolejności rosnącej, bo by obliczyć rozstęp musimy od największej liczby w naszej próbce odjąć najmniejszą.

Rozstępem badanej cechy X w próbce nazywamy różnice:

R = xmax – xmin, gdzie xmax – największa liczba ciągu, xmin – najmniejsza liczba ciągu.

Definicja rozstępu badanej cechy. *

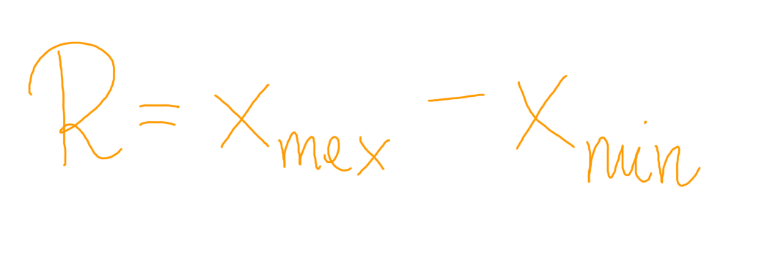
Liczymy rozstęp w naszym zadaniu.

Najmniejsza liczba w naszym zadaniu to 2.

Największa liczba w naszym zadaniu to 5.

Rozstęp wynosi:

R= 5-2=3

Ile potrzebujemy klas? Na ile przedziałów podzielimy naszą próbkę? Ile przedziałów ma mieć szereg rozdzielczy?

Mamy trzy wzory by wyliczyć na ile klas, przedziałów lub grup trzeba podzielić naszą próbkę. Najczęściej te przedziały są jednakowej długości, rzadko zdarza się, żeby przedziały były nie równej długości.

• k ≤ 5ln n
• k=1 + 3,3222 ln n
• k = √ n
• lub można spojrzeć do tabelki:

Liczymy ilość przedziałów w naszym zadaniu.

• k ≤ 5log n
  • k ≤ 5log 65
  • 5log 65 = 9,06
• k=1 + 3,3222 log n
  • k=1 + 3,3222 log 65 = 1 + 3,3222 * 1,81 = 7,02
• k = √ n
  • k = √ 65=8,06

Czyli już wiemy, że jakoś 7 a może 8 a może 9? hihi

Zaraz wszystko się wyjaśni 🙂

Buduje napięcie jak Hitchcok, ale wracajmy na ziemię. Do szeregu rozdzielczego. Jak już wiemy ile przedziałów musimy mieć, to dobrze by było wiedzieć jaką długość mają mieć przedziały w szeregu rozdzielczym?

Jaką długość mają przedziały w szeregu rozdzielczym?

Jest na to wzór! 🙂

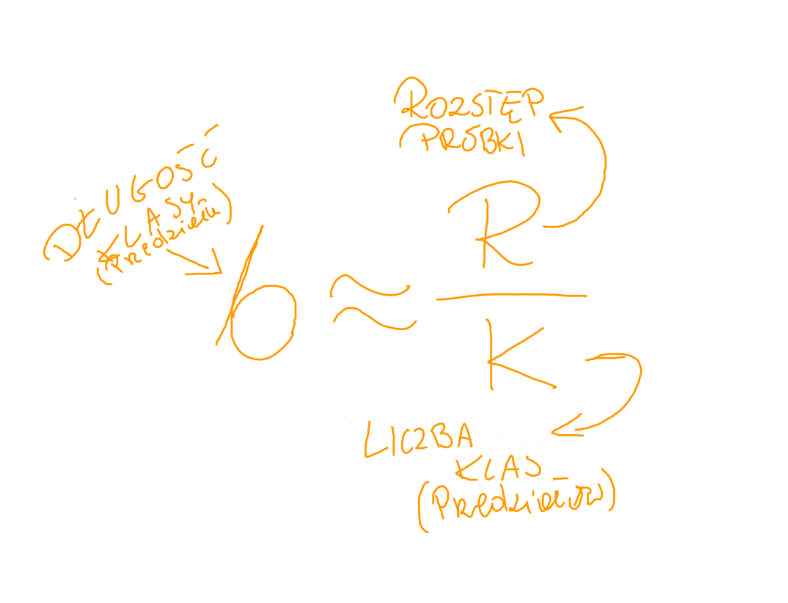
Jaką długość przedziału ma mieć szereg rozdzielczy w naszym przypadku?

Przyjmujemy, że R= 3, k=8, więc b=3 : 8 = 0,375.

Wyszło nam, że długość klasy wynosi b=0,375 dla łatwiejszych obliczeń przyjmujemy b=0,5.

Czyli już mamy wszystko.

Zbiorę co wiemy w jedno miejsce, by pominąć skrolowanie do góry ;).

Tyle liczenia i tylko tyle wiemy.

Jaką liczbę przyjmujemy jako dolną granicę naszego pierwszego przedziału w szeregu rozdzielczym?

Znów na to mamy wzór 🙂 Najczęściej jest to xmin – 0,05.

W naszym zadaniu:

xmin=2

Zatem otrzymujemy 2-0,05= 1,95.

Stworzę przedziały i zobaczycie co nam wyjdzie, i dlaczego tak, nie może być 🙂

I mam taką tabelkę

Widzimy, że wyszło nam 7 klas.

Dlaczego 7 przedziałów w szeregu rozdzielczym?

Popatrzmy na nasze dane w zadaniu, one składają się tylko z liczb 2, 3, 4, 5. I te liczby muszą nam „wpaść” do danego przedziału.

Teraz zajmę się zliczaniem ile mamy 2, 3, 4 i 5 w naszej próbce.

Ilość studentów to nasza liczebność w danym przedziale i teraz każdą z tych liczb muszę wrzucić w odpowiedni przedział.

I wyszło nam, że nie które przedziały nie mają żadnych danych, tylko samo 0. To znaczy, że musimy wydłużyć przedziały, a tym samym zmniejszyć ich ilość, bo w naszym przypadku to się nie sprawdza.

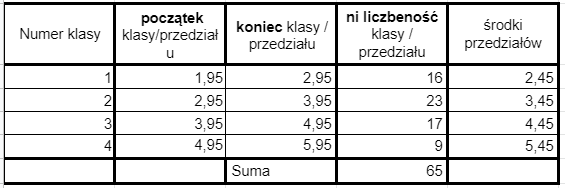
Mamy 4 klasy i one są wstanie pomieścić wszystkie nasze dane.

Jeszcze policzmy środki przedziałów, czyli średnią przedziałów.

I tak wygląda nasz szereg rozdzielczy.

I to już koniec naszego wstępu do tworzenia szeregu rozdzielczego. Teraz skupimy się na analizie struktury szeregu rozdzielczego, czyli:Miary położenia:

• średnia w szeregu rozdzielczym,
• mediana w szeregu rozdzielczym,
• moda / dominanta w szeregu rozdzielczym,
• odchylenie standardowe w szeregu rozdzielczym,
• wariancja w szeregu rozdzielczym,
• kwartyle w szeregu rozdzielczym,
• współczynnik zmienność w szeregu rozdzielczym.

Daj znać czy wszystko jasne.

A wolisz słuchać i patrzeć jak ktoś liczy zadanie to tutaj znajdziesz na YouTube jak to zadanie robię.

*Def. pochodzi z książki W.Krysicki Rachunek prawdopodobieństwa u statystyka matematyczna w zadaniach część II