Jak już wiesz jakie to są liczby naturalne, całkowite, wymierne, niewymierne i rzeczywiste, to teraz pora na liczby przeciwne. Dziś dowiesz się co to jest i jak ją wyznaczyć.

Dowiedz się co Ciebie czeka w poniższym wpisie:

1. Definicja liczb przeciwnych.
2. Przykłady
3. Liczby przeciwne na osi liczbowej
4. Przykłady
5. Liczby przeciwne zadania.
6. Rozwiązanie
7. Czy w zbiorze liczb naturalnych są liczby przeciwne?
8. Liczby przeciwne po angielsku
9. I po hiszpańsku.

Liczby przeciwne – definicja.

Liczby przeciwne to takie liczby, których suma wynosi 0. Tak nie matematycznie rzecz biorąc, liczbę przeciwną do danej liczby wyznaczasz w taki sposób, że zmieniasz jej znak i już.

Teraz trochę przykładów by liczby przeciwne były Twoim przyjacielem.

Przykłady liczb przeciwnych.

Te przykłady, które tu zobaczysz będą bazowały na tej informacji powyżej, że są to dwie liczby, których suma wynosi 0.

Przykład 1. Znajdź liczbę przeciwną do liczby 1.

I teraz pomyślmy jaka liczba dodana do 1 da mi 0?

1 + x = 0.

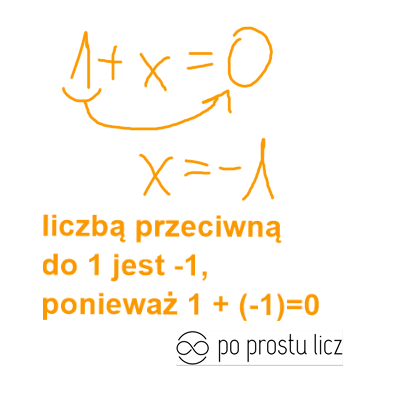
Przykład 2. Znajdź liczbę przeciwną do liczby -1/2.

Zastanówmy się razem, jaką liczbę musimy dodać do -1/2 by otrzymać 0.

PRZYKŁAD 3. Znajdź liczbę przeciwną do liczby √3.

Podobnie jak w poprzednich przykładach, zastanawiamy się jaką liczbę trzeba dodać do √3 by otrzymać liczbę 0.

PRZYKŁAD 3. Znajdź liczbę przeciwną do liczby -1+√5.

Jak myślisz jak to najłatwiej zrobić?

Ja wrzucę bardzo podobne rozwiązanie do tego co było przed chwilą, ale pod nim chcę jeszcze Tobie przypomnieć ważną rzecz o liczbach przeciwnych.

Czy można to zadanie zrobić inaczej? Ależ tak!

Wystarczy, że przed liczbę -1+√5 wstawiesz minus. Dokładnie tak -(-1+√5) i w ten sposób otrzymasz liczbę przeciwną.

-(-1+√5)= 1 – √5.

Liczbą przeciwną do liczby -1+√5, jest liczba 1 – √5, ponieważ -1+√5 + 1 – √5=0.

Też możesz spotkać się jeszcze z jedną definicją, która dotyczy osi liczbowej i odległości od 0.

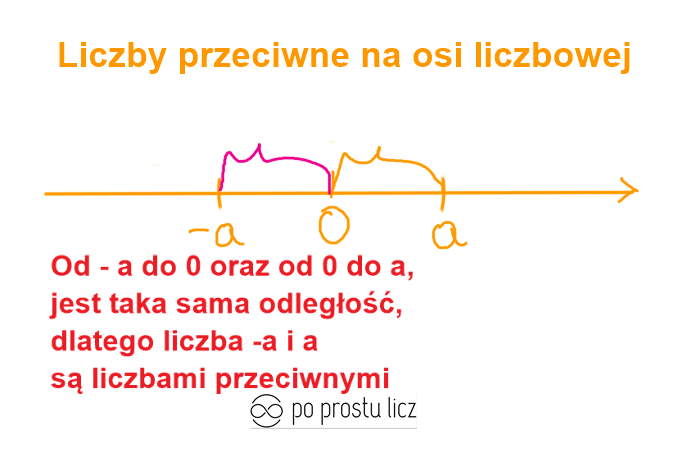
Liczby przeciwne na osi liczbowej.

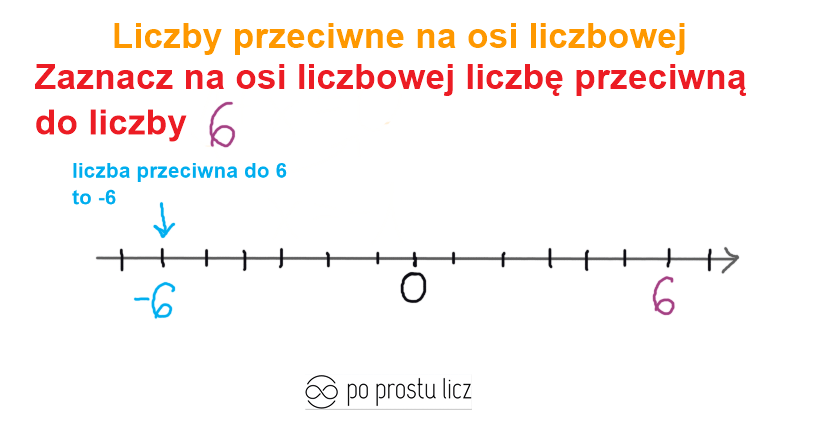
Liczby przeciwne to takie dwie liczby leżące na osi liczbowej w tej samej odległości od zera, lecz po przeciwnych stronach.

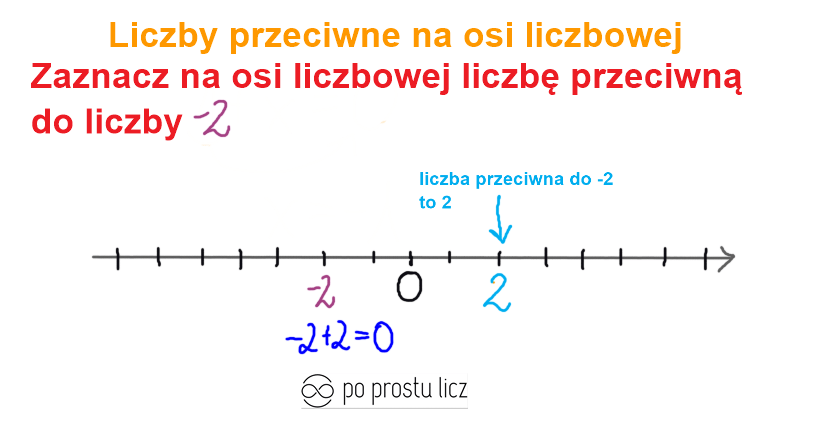
Przykład 1. Na osi liczbowej zaznacz liczby przeciwne do liczby:

a) -2

b) 6

Liczby przeciwne zadania.

Wyznacz liczbę przeciwną do podanych liczb:

• 2
• -13
• 13/21
• -21/30
• √2
• -√2
• 0

Rozwiązanie zadań.

Rozwiązanie zadań znajdziesz klikając TUTAJ, przeniesie Ciebie na YouTube gdzie czeka na Ciebie wytłumaczone zadanie krok po kroku.

Możesz kliknąć w obrazek poniżej by zobaczyć rozwiązania.

Liczby przeciwne po angielsku.

Czasem mamy ochotę poszukać danego słowa w innym języku:

• the additive inverse of a number,
• the opposite (number),
• sign change,
• negation.

Liczby przeciwne po hiszpańsku.

W Hiszpanii również dzieci się uczą o liczbach i na liczby przeciwnę mówią:

• el opuesto o simétrico para la suma,
• inverso aditivo.

Czy zbiorze liczb naturalnych są liczby przeciwne?

Zacznijmy od tego, czym tak naprawdę są liczby naturalne, by zrozumieć jak to dokładniej działa.

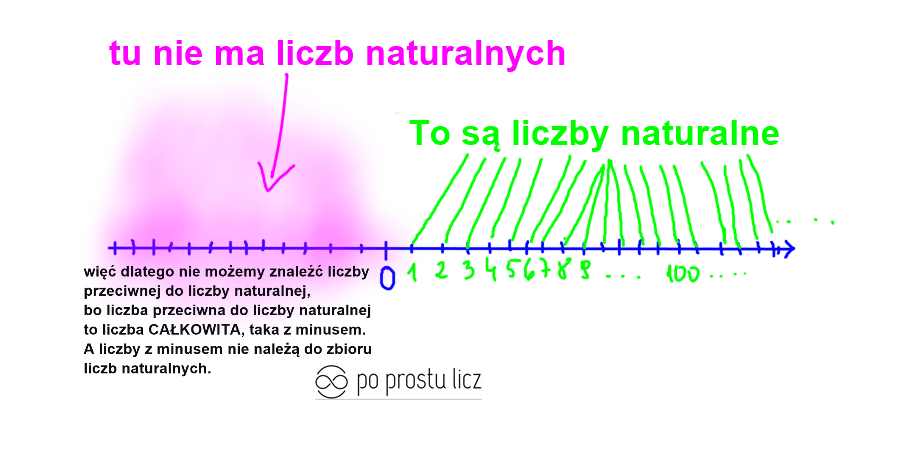
Liczby naturalne (o liczbach naturalnych doczytaj tutaj KLIK KLIK), to takie całe liczby, bez minusów, bez ułamków, bez pierwiastków etc. służą nam do podania ilości oraz ustalenia kolejności, dlatego nie możemy powiedzieć, że w kolejce do sklepu stoi 10,5 człowieka ;).

I właśnie dlatego w zbiorze liczb naturalnych NIE MA liczb przeciwnych.

Widzisz to?

No dobra… to jeszcze raz i powoli.

Liczby naturalne to takie liczby:

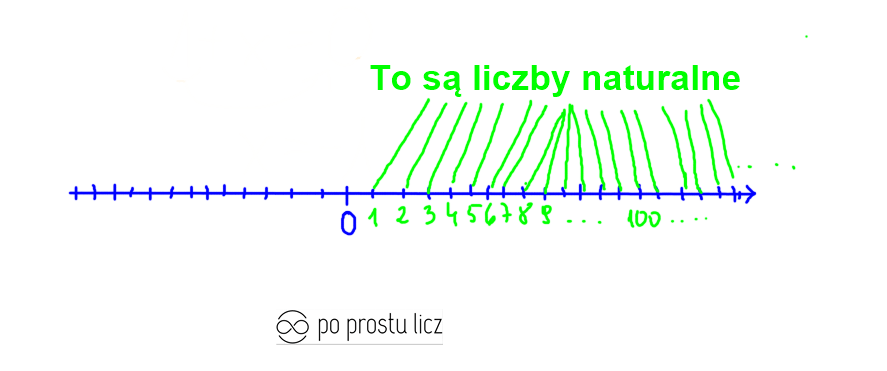
I jak już wiesz liczby przeciwne to taka para liczb, z których jedna ma minus a druga plus, a liczby ujemne, te z minusem mieszkają z lewej strony zera, a tam znów nie ma liczb naturalnych. Mamy taką sytuację

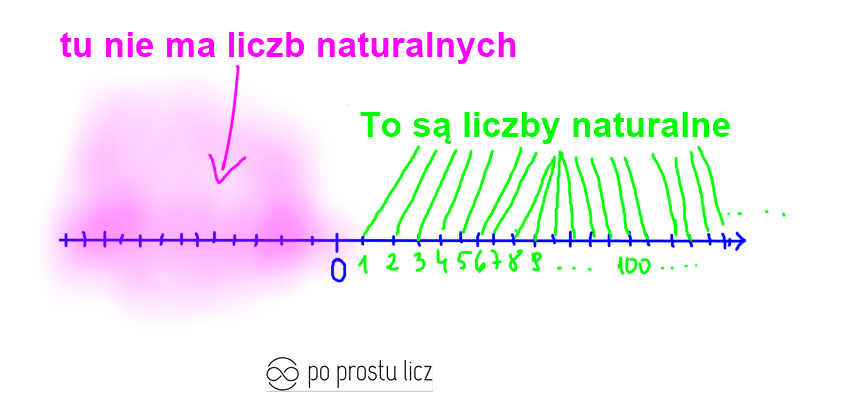
Nie możemy znaleźć liczby przeciwnej do liczby naturalnej, ponieważ liczba przeciwna do liczby naturalnej musi znajdować się po drugiej stronie osi liczbowej, mam na myśli na lewo od zera. Na lewo od zera mamy liczby ujemne, czyli takie z minusem, a takie liczby nazywamy liczbami całkowitymi.

Podsumowując jednym zdaniem: w zbiorze liczb naturalnych nie ma liczb przeciwnych, ponieważ liczby naturalne nie zawierają liczb ujemnych.