Kombinatoryka, reguła mnożenia, kombinacje, wariacje i inne cuda wianki. Tak to wszystko wchodzi w skład kombinatoryki.

Jak rozwiązywać zadania z kombinatoryki?

To pytanie często zadają mi moi uczniowie, jak mam to policzyć bez pani. Jak mam na to wpaść? Dlaczego te zadania z kombinatoryki są takie dziwne.

Ja zalecam po prostu sobie wszystko krok po kroku rozpisać. Jeśli zadanie dotyczy ile liczb dwu/trzy/czetro-cyfrowych mamy, które spełniają jakieś tam założenie, to zacznij je robić od zastanowienia się ile cyfr występuje w tej liczbie. Ja wiem, brzmi to zabawnie, aleeee w stresie popełniamy różne błędy, a na maturze jest stresu kuuupa!

Nim przejdziemy do konkretów szybkie podsumowanie.

Skocz szybko w miejsce, które Ciebie interesuje

Permutacje | Kombinacje | Wariacje z powtórzeniami | Wariacje bez powtórzeń | Liczby w kombinatoryce | Zadania maturalne

Permutacja – zastosowanie silni w kombinatoryce

Silnie, która nosi też przydomek permutacje stosujemy m.in. gdy z treści zadania wynika, że

• przestawiamy litery w pewny wyrazie różnoliterowym,
• ustawiamy osoby w szeregu lub sadzamy je w koło ,
• przestawiamy cyfry w liczbie, uwzględniając pewne warunki.

Przykładowe zadanie z permutacją:

1. Na ile sposobów można ustawić w kolejce do kasy biletowej 6 osób?
2. Ile połączeń ośmioliterowych, będących wyrazami lub nie, można utworzyć z liter wyrazu klapa?
3. Na ile sposobów można posadzić 8 osób na ośmiu numerowanych miejscach?
4. Ile różnych liczb pięciocyfrowych takich, aby żadna cyfra w liczbie nie powtarzała się można utworzyć z cyfr: 0, 1, 2, 3, 4?

Kombinacje, jak ich używać w kombinatoryce?

Kombinacje stosujemy wtedy, gdy z treści zadania wynika, że

• losowanie odbywa się bez zwracania
• kolejność wylosowanych elementów jest nieistotna

Przykładowe zadania z kombinacjami

1. Na egzaminie maturalnym uczeń wybiera 3 zadania spośród 10. Na ile sposobów może to zrobić?
2. Trener siatkarzy ma do dyspozycji dwunastoosobową grupę treningową. Na ile sposobów może wybrać sześcioosobową drużynę?
3. Z talii 52 kart losujemy bez zwracania 8 kart. Ile jest możliwych wyników losowania, w których są dokładnie 3 walety i 3 damy.

Wariacje bez powtórzeń, kiedy je używamy? Wariacje w kombinatoryce.

Wariacje bez powtórzeń stosujemy wtedy, gdy z treści zadania wynika, że:

• losowanie odbywa się bez zwracania
• kolejność wylosowanych elementów jest istotna.

Przykładowe zadania:

1. Oblicz ile jest liczb pięciocyfrowych o niepowtarzających się cyfrach.

2. Ile jest możliwości posadzenia 6 osób na 10 krzesłach ustawionych w rzędzie.

Wariacje z powtórzeniami o co z nimi chodzi i kiedy stosujemy je w zadaniach z kombinatoryki?

Wariacje z powtórzeniami stosujemy wtedy gdy z treści zadania wynika, że

• losowanie odbywa się ze zwracaniem
• kolejność wylosowanych elementów jest istotna.

Przykładowe zadania:

1. Na ile sposobów można umieścić w 9 szufladach 4 bluzki?
2. Na ile sposobów można umieścić w 4 szufladach 9 bluzek?

Liczba dwucyfrowa, czyli jaka?

Liczba dwucyfrowa składa się z dwóch cyfr:

• cyfry dziesiątek
• cyfry jedności.

Na przykład:

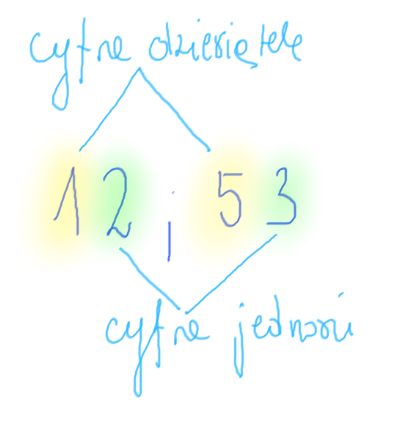
• Liczba 12 – 1 to cyfra dziesiątek, 2 to cyfra jedności.
• Liczba 53 – 5 to cyfra dziesiątek, 3 to cyfra jedności.

Liczby dwucyfrowe zaczynają się od 10 a kończą się na 99. Wszystko pomiędzy 10 a 99 należy do liczb dwucyfrowych.

Liczba trzycyfrowa, czyli jaka?

Liczby trzycyfrowa składa się z trzech cyfr:

• cyfry setek,
• cyfry dziesiątek,
• cyfry jedności.

Na przykład

• Liczba 123 – 1 to cyfra setek 2 to cyfra dziesiątek, 3 to cyfra jedności.
• Liczba 679 – 6 to cyfra setek 7 to cyfra dziesiątek, 9 to cyfra jedności.

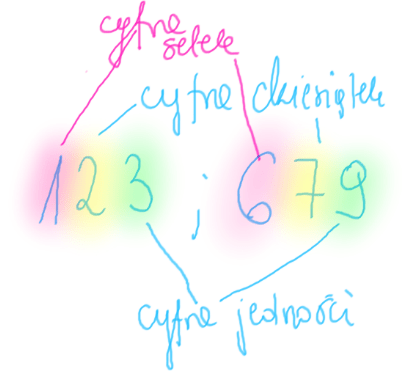
Liczby trzycyfrowe zaczynają się od 100 a kończą się na 999. Wszystko pomiędzy 100 a 999 należy do liczb dwucyfrowych.

Liczba czterocyfrowa, czyli jaka?

Liczby trzycyfrowa składa się z trzech cyfr:

• cyfry tysięcy
• cyfry setek,
• cyfry dziesiątek,
• cyfry jedności.

Na przykład

• Liczba 4123 – 4 to cyfra tysięcy, 1 to cyfra setek 2 to cyfra dziesiątek, 3 to cyfra jedności.
• Liczba 2679 – 2 to cyfra tysięcy, 6 to cyfra setek 7 to cyfra dziesiątek, 9 to cyfra jedności.

Przygotowałam dla Ciebie serię filmików powtórzeniowych. Tutaj wrzucę listę z zadaniami. Najpierw zmierz się z nimi sam/a a potem zobacz jak ja to robię.

Kolejną ważna sprawą są cechy podzielności liczb.

Cechy podzielności liczb:

ZADANIE 1. to zadanie numer 13 z matury SIERPIEŃ 2011 poziom podstawowy
Ile jest liczb naturalnych czterocyfrowych o sumie cyfr równej 2?
A) 1 B) 2 C) 3 D) 4

ZADANIE 2. to zadanie numer 24 z matury MAJ 2012 poziom podstawowy
Flagę, taką jak pokazano na rysunku, należy zszyć z trzech jednakowej szerokości pasów kolorowej tkaniny. Oba pasy zewnętrzne mają być tego samego koloru, a pas znajdujący się między nimi ma być innego koloru. Liczba różnych takich flag, które można uszyć, mając do dyspozycji tkaniny w 10 kolorach, jest równa
A) 100 B) 99 C) 90 D) 19

ZADANIE 3. to zadanie numer 15 z matury SIERPIEŃ 2013 poziom podstawowy
Ile jest wszystkich liczb naturalnych trzycyfrowych podzielnych przez 5?
A) 90 B) 100 C) 180 D) 200

ZADANIE 4. to zadanie numer 24 z matury MAJ 2014 poziom podstawowy
Na ile sposobów można wybrać dwóch graczy spośród 10 zawodników?
A) 100 B) 90 C) 45 D) 20

ZADANIE 5. to zadanie numer 24 z matury CZERWIEC 2014 poziom podstawowy
Ile jest wszystkich liczb naturalnych dwucyfrowych podzielnych przez 6 i niepodzielnych przez 9?
A) 6 B) 10 C) 12 D) 15

ZADANIE 6. to zadanie numer 24 z matury CZERWIEC 2014 poziom podstawowy technikum
Ile jest wszystkich liczb naturalnych trzycyfrowych, których iloczyn cyfr jest równy 4?
A) 3 B) 4 C) 6 D) 8

Jeśli szukasz rozwiązań to jeszcze raz wkleję link TUTAJ.

Druga część powtórki

ZADANIE 1. to zadanie numer 25 z matury SIERPIEŃ 2015 poziom podstawowy
Ile jest wszystkich liczb czterocyfrowych, większych 3000, utworzonych wyłącznie z cyfr 1, 2, 3, przy założeniu, że cyfry mogą się powtarzać, ale nie wszystkie z tych cyfr muszą być wykorzystane?
A) 3 B) 6 C) 9 D) 27

ZADANIE 2. to zadanie numer 25 z matury SIERPIEŃ 2016 poziom podstawowy
Ile jest wszystkich dwucyfrowych liczb naturalnych podzielnych przez 3?
A) 12 B) 24 C) 29 D) 30

ZADANIE 3. to zadanie numer 24 z matury SIERPIEŃ 2017 poziom podstawowy
Ile jest wszystkich czterocyfrowych liczb naturalnych mniejszych niż 2017?
A) 2016 B) 2017 C) 1016 D) 1017

ZADANIE 4. to zadanie numer 24 z matury MAJ 2018 poziom podstawowy
Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2018 i podzielnych przez 5?
A) 402 B) 403 C) 203 D) 204

ZADANIE 5. to zadanie numer 24 z matury CZERWIEC 2018 poziom podstawowy
Liczba wszystkich dodatnich liczb czterocyfrowych parzystych, w których zapisie nie występują cyfry 0 i 2, jest równa
A) 8 ⋅8⋅ 8⋅3 B) 8⋅7 ⋅6 ⋅3 C) 8 ⋅10⋅ 10⋅ 4 D) 9 ⋅8⋅ 7⋅4

ZADANIE 6. to zadanie numer 24 z matury MAJ 2019 poziom podstawowy
Wszystkich liczb pięciocyfrowych, w których występują wyłącznie cyfry 0, 2, 5, jest
A) 12 B) 36 C) 162 D) 243

ZADANIE 7. to zadanie numer 21 z matury CZERWIEC 2019 poziom podstawowy
Liczb naturalnych dwucyfrowych podzielnych przez 6 jest
A) 60 B) 45 C) 30 D) 15

ZADANIE 8. to zadanie numer 24 z matury SIERPIEŃ 2019 poziom podstawowy
Wszystkich liczb naturalnych czterocyfrowych parzystych, w których występują wyłącznie cyfry 1, 2, 3, jest
A) 54 B) 81 C) 8 D) 27

Jeśli nie wiesz gdzie są rozwiązania – znajdziesz je TUTAJ.

Jak jeszcze Ciebie coś gnębi w tym temacie to pisz!

I jeszcze dorzucę Tobie super temat, czyli permutacje! 🙂