Silnia jest bardzo ważna w kombinatoryce, gdy liczymy permutacje, wariacje bez powtórzeń, kombinacje tam właśnie pojawia się ona silnia. Dziś dowiesz się co to jest silnia, co to jest permutacja i kiedy to wszystko stosujemy, innym razem skupimy się na kombinacjach czy wariacjach.
Reguła mnożenia
Wynik pewnego działania zależy od kolejno podejmowanych decyzji, to stosujemy regułę mnożenia.
Jak ona działa?
Jeśli podejmujemy jedną decyzję i mamy do wyboru n1 możliwości, przy podjęciu kolejnej decyzji mamy n2, itd.. aż do ostatnie decyzji, gdy mamy nk możliwości, to liczba różnych wyników, które możemy otrzymać wynosi:
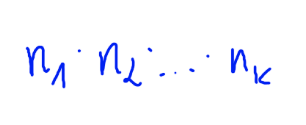
Przykłady zastosowania reguły mnożenia:
W urnie znajduje się 7 kul ponumerowanych cyframi od 1 do 7.
- wyciągamy kolejno wszystkie kule, zapisując wylosowane cyfry. Ile różnych siedmiocyfrowych liczb można w ten sposób utworzyć?
- Pierwsza kula zostanie wylosowana jedna kula z siedmiu, czyli mam 7 możliwości
- Druga kula zostanie wylosowana jedna kula z sześciu, już jedną wylosowaliśmy więc w urnie zostało 7-1=6 kul, czyli mamy 6 możliwości.
- Trzecia kula zostanie wylosowana jedna kula z pięciu, już jedną wylosowaliśmy więc w urnie zostało 6-1=5 kul, czyli mamy 5 możliwości.
- Czwarta kula zostanie wylosowana jedna kula z czterech, już jedną wylosowaliśmy więc w urnie zostało 5-1=4 kul, czyli mamy 4 możliwości.
- Piąta kula zostanie wylosowana jedna kula z czterech, już jedną wylosowaliśmy więc w urnie zostało 4-1=3 kul, czyli mamy 3 możliwości.
- Szósta kula zostanie wylosowana jedna kula z trzech, już jedną wylosowaliśmy więc w urnie zostało 3-1=2 kul, czyli mamy 2 możliwości.
- Siódma kula zostanie wylosowana jedna kula z pięciu, już jedną wylosowaliśmy więc w urnie zostało 2-1=1 kul, czyli mamy 1 możliwość.
- Zatem różnych liczb siedmiocyfrowych, jakie możemy otrzymać jest: 7*6*5*4*3*2*1.
- wyciągamy kolejno trzy kule z urny, zapisując wylosowane cyfry. Ile różnych trzycyfrowych liczb można w ten sposób utworzyć?
- Pierwsza kula zostanie wylosowana jedna kula z siedmiu, czyli mam 7 możliwości.
- Druga kula zostanie wylosowana jedna kula z sześciu, już jedną wylosowaliśmy więc w urnie zostało 7-1=6 kul, czyli mamy 6 możliwości.
- Trzecia kula zostanie wylosowana jedna kula z pięciu, już jedną wylosowaliśmy więc w urnie zostało 6-1=5 kul, czyli mamy 5 możliwości.
- Zatem różnych liczb trzycyfrowych, jakie możemy otrzymać jest: 7*6*5.
- losujemy trzy kule, po wylosowaniu każdej kuli zapisujemy cyfrę, a kulę wrzucamy z powrotem do urny. Ile jest różnych możliwości?
- Pierwsza kula zostanie wylosowana jedna kula z siedmiu, czyli mam 7 możliwości,
- Druga kula zostanie wylosowana jedna kula z siedmiu, pierwszą kulę, którą wylosowaliśmy, wrzuciliśmy powrotem do urny, dlatego cały czas mamy do wyboru 7 kul.
- Trzecia kula zostanie wylosowana jedna kula z siedmiu, drugą kulę, którą wylosowaliśmy, wrzuciliśmy powrotem do urny, dlatego cały czas mamy do wyboru 7 kul.
- Zatem różnych liczb trzycyfrowych, jakie możemy otrzymać jest: 7*7*7.
Co to jest silnia?
Silnia to iloczyn kolejnych liczb naturalnych.
Definicja silni
Silnia to funkcja przyporządkowująca każdej liczbie naturalnej n, liczbę n!, określoną wzorem:
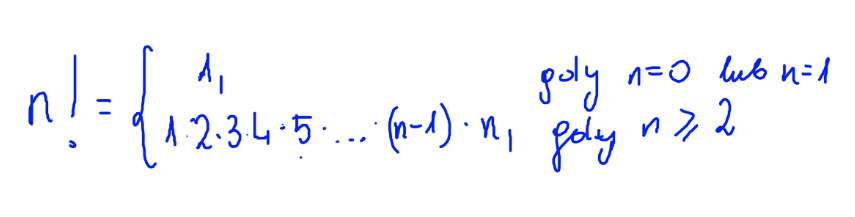
Przykłady obliczania silni
0! = 1
1! = 1
2! =1· 2 = 2
5!= 1· 2 · 3· 4· 5= 120
Permutacja
Permutacją n elementów nazywamy każdy ciąg n-wyrazowy utworzony ze wszystkich elementów danego zbioru.
Liczba permutacji n-elementowego zbioru wyraża się wzorem:
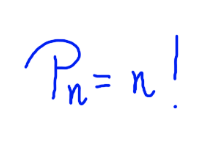
Często nie spotkasz się z poznaczeniem permutacji jako Pn, najczęściej po prostu piszemy permutację od razu jako silnie.
Kiedy stosujemy permutacje? W jakich zadaniach?
Permutacje stosujemy m.in. gdy z treści zadania wynika, że:
- przestawiamy litery w pewny wyrazie różnoliterowym,
- ustawiamy osoby w szeregu lub sadzamy je w koło,
- przestawiamy cyfry w liczbie, uwzględniając pewne warunki.
Przykładowe zadania dotyczące permutacji i więcej silni
- Na ile sposobów można ustawić w kolejce do kasy biletowej 6 osób? 6!
- Ile połączeń ośmioliterowych, będących wyrazami lub nie, można utworzyć z liter wyrazu komputer? Słowo komputer ma 8 liter, więc możemy utworzyć 8!.
- Fotograf ustawia do zdjęcia rodziców i trójkę dzieci. Na ile sposobów może to, zrobić jeżeli: a) rodzice i dzieci stoją w jednym rzędzie b) wszyscy stoją w jednym rzędzie, z tym że rodzice stoją obok siebie, c) rodzice stoją w pierwszym rzędzie, a dzieci w drugim.
- Na ile sposobów można rozdać trzem finalistom 3 różne nagrody? 3!
- Na ile sposobów możemy ułożyć 8 książek jedna na drugiej? 8! sposobów.
I to już na tyle.
Dużo informacji, dużo przykładów. Jeśli masz ochotę na więcej to zapraszam do przejrzenia poniższej listy:
Lista zadań dotycząca permutacji, reguły mnożenia, silnia.
- Wszystkich liczb naturalnych pięciocyfrowych parzystych jest A.9⋅2⋅103 B.9⋅5⋅103 C.5⋅104 D.4⋅105
- Rozwiązanie znajdziesz tutaj KLIK
- Wszystkich czterocyfrowych liczb naturalnych, w których cyfra tysięcy i cyfra setek są większe od 4, a każda z pozostałych cyfr jest mniejsza od 6, jest: A) 4⋅4⋅5⋅5 B) 5⋅4⋅6⋅5 C) 5⋅5⋅6⋅6 D) 4⋅3⋅5⋅4
- Rozwiązanie znajdziesz tutaj KLIK
- Wszystkich liczb naturalnych trzycyfrowych, większych od 700, w których każda cyfra należy do zbioru {1, 2, 3, 7, 8, 9} i żadna cyfra się nie powtarza, jest A. 108 B. 60 C. 40 D. 299
- Rozwiązanie znajdziesz tutaj KLIK
- Ilość wszystkich liczb czterocyfrowych, w których cyfry się nie powtarzają, wynosi:
- Rozwiązanie znajdziesz tutaj KLIK
- Wszystkich liczb naturalnych trzycyfrowych parzystych, w których cyfra 7 występuje dokładnie jeden raz, jest A. 85 B. 90 C. 100 D. 150
- Rozwiązanie znajdziesz tutaj KLIK
- Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2020 i podzielnych przez 4? A) 506B) 505C) 256D) 255
- Rozwiązanie znajdziesz tutaj KLIK
- Wszystkich liczb naturalnych czterocyfrowych parzystych, w których występują wyłącznie cyfry 1,2,3 jest: A) 54 B) 81 C) 8 D) 27
- Rozwiązanie znajdziesz tutaj KLIK
- Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2018 i podzielnych przez 5? A) 402 B) 403 C) 203 D) 204
- Rozwiązanie znajdziesz tutaj KLIK
- Wszystkich liczb pięciocyfrowych, w których występują wyłącznie cyfry 0,2,5, jest: A) 12 B) 36 C) 162 D) 243
- Rozwiązanie znajdziesz tutaj KLIK
- Ile jest wszystkich dwucyfrowych liczb naturalnych utworzonych z cyfr: 1, 3, 5, 7, 9, w których cyfry się nie powtarzają? A) 10 B) 15 C) 20 D) 25
- Rozwiązanie znajdziesz tutaj KLIK
I teraz już zamykamy temat 🙂 w tym miejscu masz cała playliste z powyższymi zadaniami, jeśli wolisz od razu przejść do rozwiązań KLIK.
Ah i jeszcze jedno! Jeśli masz ochotę na naukę do matury, to zapraszam Ciebie na 15 minut do matury lub na kurs.
Madre mia! Ostatnia już rzecz, obiecuje!
Gdy masz ochotę powtórzyć zadania z kombinatoryki, które były na maturze, to możesz zerknąć w to miejsce:
Bibliografia:
Definicja silni i permutacji pochodzi z książki ISBN 83-869444-49-8, Wydawnictwo SENS.




