Funkcja liniowa pierwsza „poważna” funkcja z którą się spotykasz na swojej matematycznej drodze. Ma charakterystyczny wzór y=ax+b, ale o tym jeszcze porozmawiamy. Poniżej umieszczam spis treści by łatwiej się Tobie poruszało po tej pomocy.

1. Definicja funkcji liniowej
2. Wzór funkcji.
3. Równanie ogólne.
4. Równanie kierunkowe.
5. Punkt przecięcia z osią OX.
   • Jak obliczyć punkt przecięcia funkcji liniowej z osią OX?
   • Miejsce zerowe funkcji liniowej.
6. Punkt przecięcia z osią OY
   • Jak obliczyć punkt przecięcia funkcji liniowej z osią OY?
7. Zadania do rozwiązania z punktem przecięcia osi.
8. Monotoniczność funkcji liniowej, czyli kiedy rośnie, maleje lub jest stała.
   • Zadania.
9. Funkcja rosnąca
   • Przykłady.
   • Wykres.
   • Zadania.
10. Funkcja malejąca.
    • Przykłady.
    • Wykres.
    • Zadania.
11. Funkcja stała
    • Przykłady.
    • Wykres.
    • Zadania.
12. Wykres funkcji liniowej. Krok po kroku.

Definicja funkcji liniowej – co to jest funkcja liniowa?

Funkcję liniową określoną wzorem

f(x)=ax+b, gdzie a ∈ R, b ∈ R, x ∈ R

nazywamy funkcją liniową.

Wzór funkcji liniowej

Funkcję liniową znamy z takich postaci:

• y=ax+b,
• Ax+By+C=0.

I najczęściej korzystamy z tego pierwsze wzoru.

Postać ogólna funkcji liniowej

Równanie ogólne prostej:
Ax +By + C = 0,
gdzie A² + B² ≠ 0, to znaczy, że A i B nie mogą w tym samym momencie wynosić 0.

I teraz mamy kilka własności:

• A = 0, to prosta jest równoległa do osi Ox,
• B = 0, to prosta jest równoległa do osi Oy,
• C = 0, to prosta przechodzi przez początek układu współrzędnych.

Poniżej możesz zobaczyć przykład, że to co jest tu napisane to prawda 🙂

Jak na wykresie można przedstawić funkcję liniową za pomocą postaci ogólnej?

• Pierwszy wzór : 5x+2=0 dotyczy przypadku gdy B=0.
• Drugi wzór 2y+4=0 to A=0.
• Trzeci wzór 2x+4y=0, to przypadek gdy C=0.
• A czwarty wzór 3x-8y-12=0, ro przykład gdy mamy wszystkie współczynniki.

Funkcja liniowa i jej postać kierunkowa funkcji liniowej

Ją znamy i kochamy! Wygląda tak!

y=ax+b,

gdzie

• a to współczynnik kierunkowy,
• b to punkt przecięcia z osią OY.

Jak na wykresie można przedstawić funkcję liniową za pomocą postaci ogólnej?

Punkt przecięcia funkcji liniowej z osią OX.

Jest to punkt na osi OX. Dokładnie taki gdzie nasz y zawsze przyjmuje wartość 0. Jeśli nadal brzmi to dla Ciebie jak bla bla bla, poczekaj zaraz na wykresach zobaczysz o co chodzi.

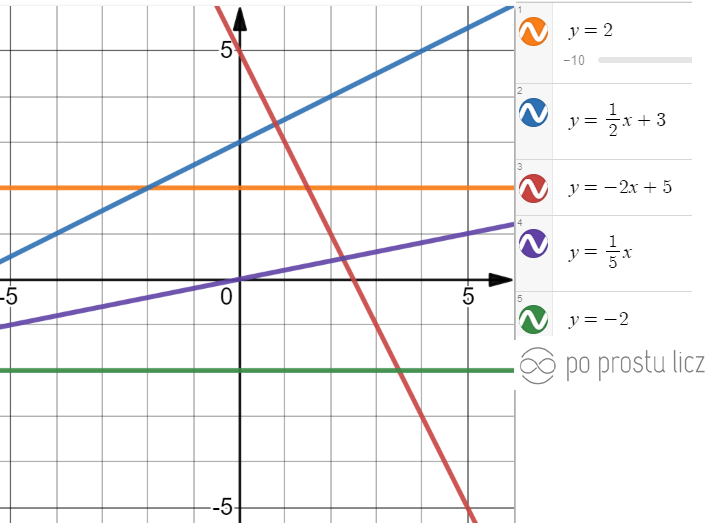
Najpierw spójrz na funkcje, które są na wykresie, jest ich kilka by było ciekawiej.

W powyższym układzie współrzędnych możemy znaleźć oto te funkcje liniowej.

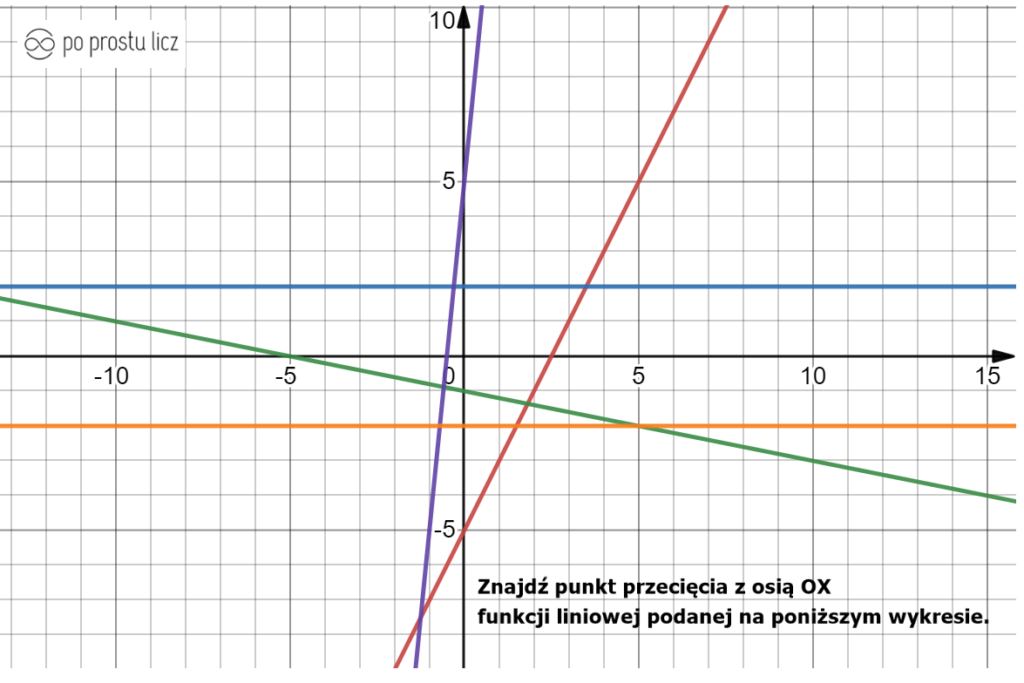
Następnie zaznaczę oś OX.

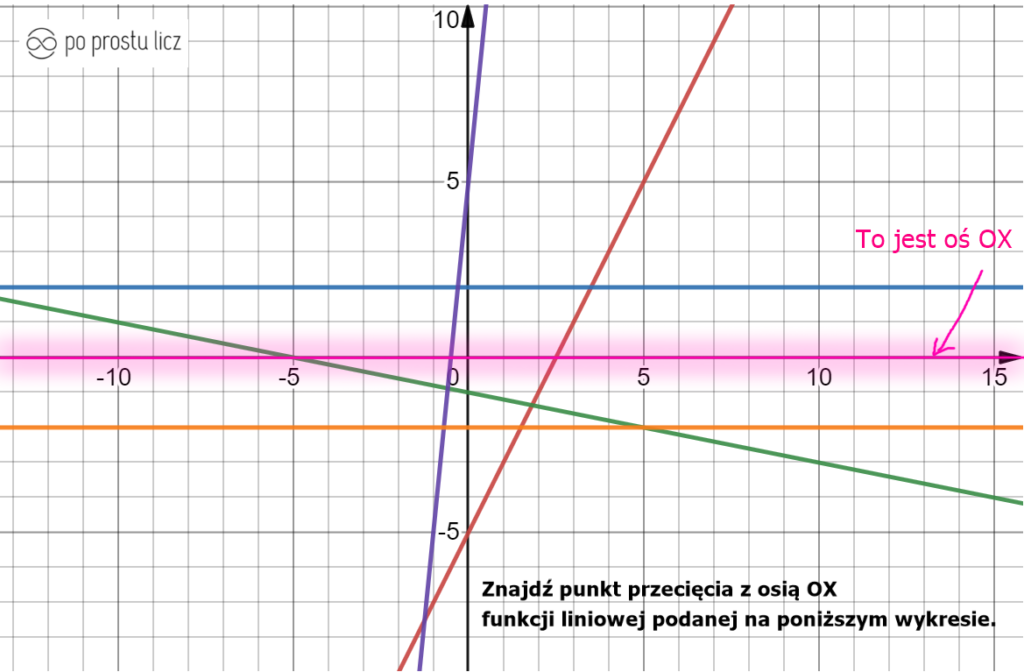
I jak już wiemy, który kreska to oś OX, to teraz mogę zaznaczyć punkty wspólne dla danej funkcji liniowej i osi OX, te miejsca zaznaczyłam zielonymi kropkami.

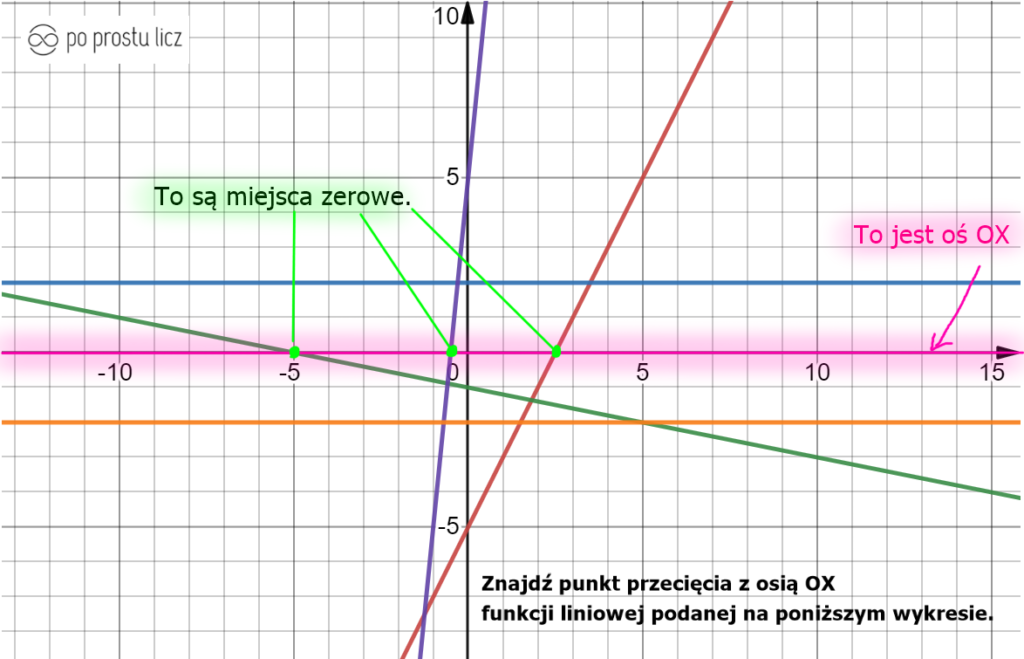
Kolejne pytanie jakie się nasuwa to:

Czy każda funkcja liniowa ma punkt przecięcia z osią OX?

Nie. Spójrz na wykres jeszcze raz, ja na nim zaznaczyłam dwie funkcje, dość specyficzne i to właśnie one nie mają punktu przecięcia z osią OX.

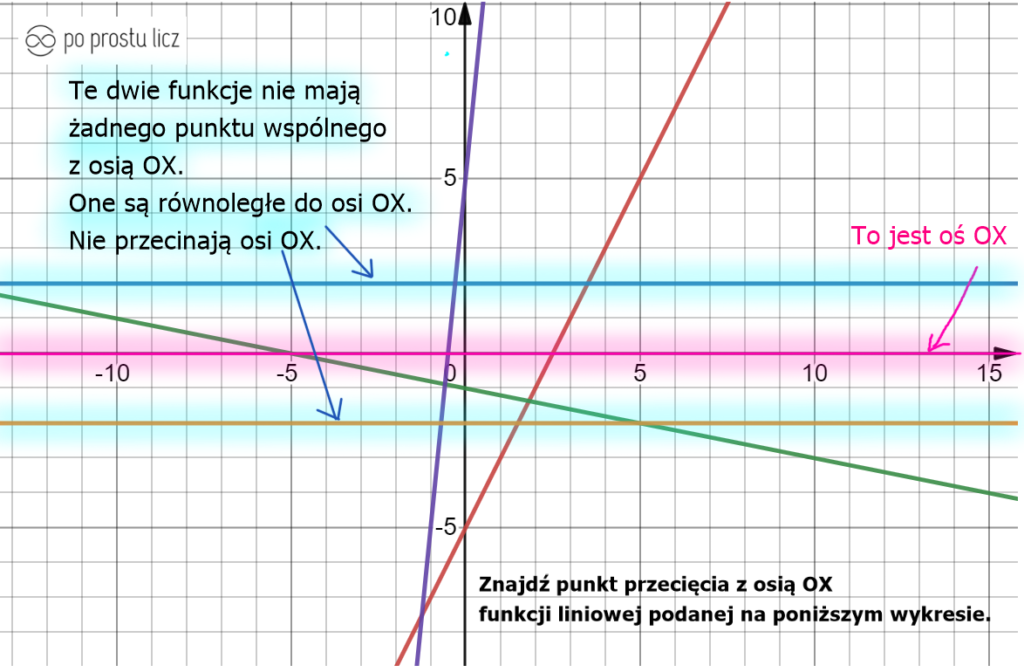
Jak obliczyć punkt przecięcia funkcji liniowej z osią OX?

Już wiesz, który to punkt przecięcia na wykresie, inaczej mówiąc, wiesz jak szukać punktu przecięcia z osią OX, ale jak nie mam wykresu, to jak wtedy obliczyć ten punkt? Spójrz jeszcze raz na wykres, tym razem na wykres na niosłam dokładne współrzędne jakie mają dane punkty przecięcia z osią OX.

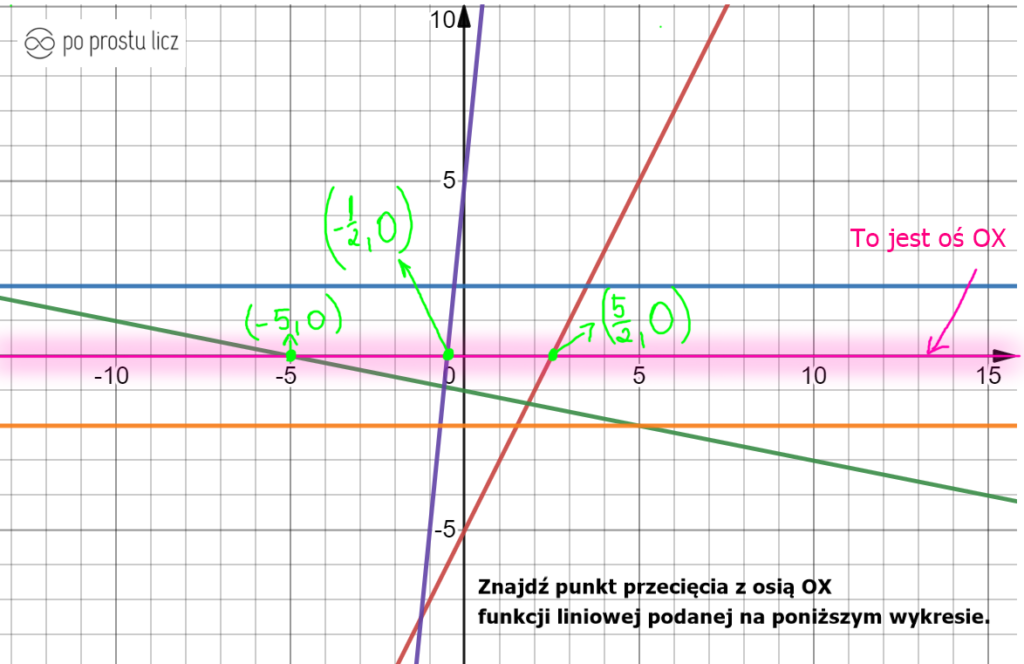
Każdy z tych punktów ma jedną rzecz wspólną, mianowicie współrzędna y wszędzie jest równa 0, więc by obliczyć punkt przecięcia z osią OX wystarczy za y lub f(x) dać 0.

Miejsce zerowe funkcji liniowej.

To punkt przecięcia osi OX, te dwie nazwy są stosowane zamienne. Jeśli w treści zadania masz do obliczenia miejsce zerowe obliczamy dokładnie tak samo jak punkt przecięcia osi OX, czyli za y lub f(x) podstawiamy 0 i już, po robocie. Wrzucę Tobie kolejną dawkę zadań.

Punkt przecięcia z osią OY funkcji liniowej.

Już wiesz co to punkt przecięcia z osią OX, to teraz popatrzymy gdzie dana funkcja ma punkt przecięcia z osią OY. Najpierw zaznaczę na dobry początek oś OY, by było łatwiej szukać miejsc przecięć z funkcjami.

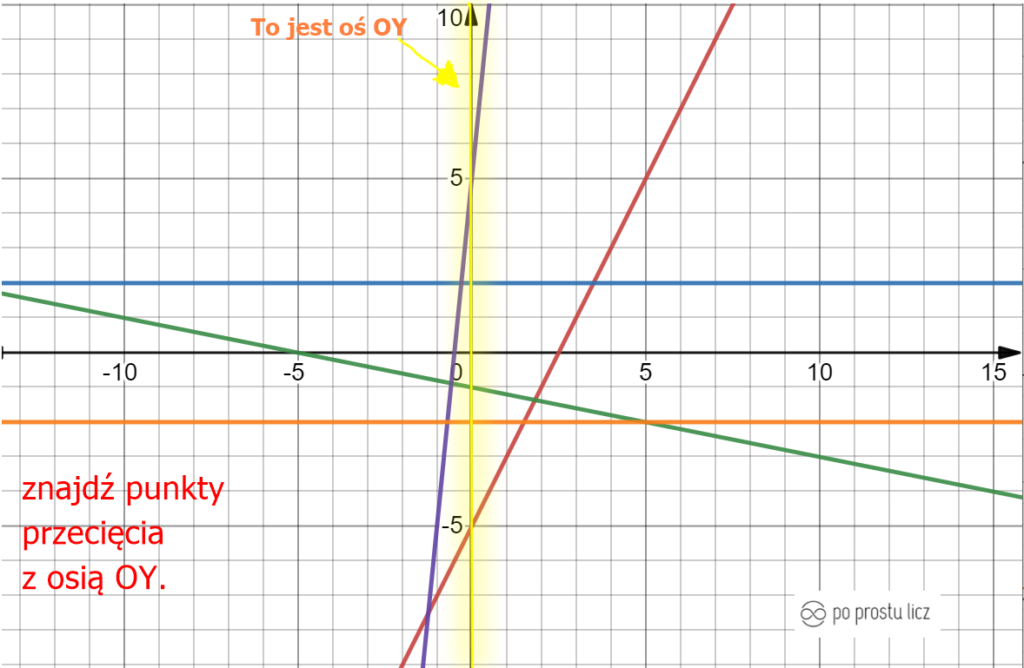
Gdy już wiemy, która to oś OY teraz trzeba odszukać te wszystkie punkty na osi OY, ja to zrobiłam i zaznaczyłam na kolor niebieski.

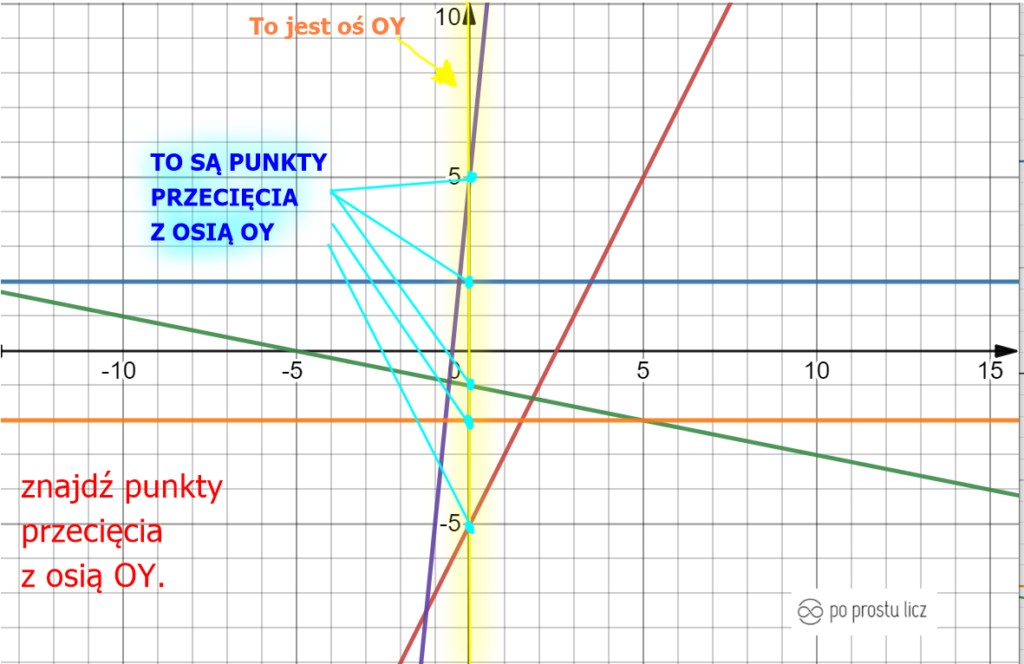
Podobnie jak w poprzedniej części dotyczącej osi OX, wpada nam pytanie jak to obliczyć gdy nie mamy wykresu.

Jak obliczyć punkt przecięcia funkcji liniowej z osią OY?

Punkt przecięcia z osią OY, to taki punkt gdzie współrzędna x zawsze wynosi 0, czyli żeby obliczyć punkt przecięcia z osią OY wystarczy za x dać 0 i wyliczyć wartość dla y.

Przykłady obliczonego punktu przecięcia funkcji liniowej z osią OY.

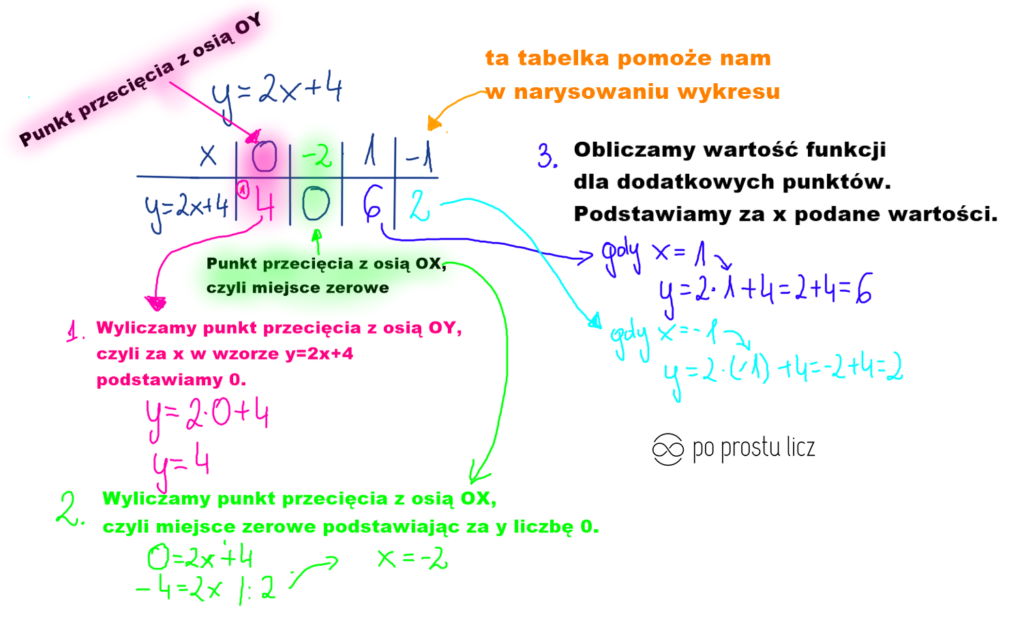
Zauważ, że to o czym wspominałam trochę wyżej o tutaj jest prawdą, że to nasze b, czyli ta liczba bez x jest punktem przecięcia z osią OY, więc nie musisz wyliczać możesz od razu napisać ten punkt. Spójrz na poniższy przykład.

Jak obliczyć punkt przecięcia z osią OY bez obliczania równania?

Tutaj bez żadnych ceregieli wrzucam rowiązanych kilka przykładów, pozaznaczałam co skąd się bierze.

Zadania z funkcji liniowej oblicz punkt przecięcia z osiami układów współrzędnych.

Poniżej czeka na Ciebie praktyka, najpierw spróbuj sam policzyć zadania, a potem sprawdź czy masz tak jak ja.

Powodzenia!

Funkcja liniowa i jej wykres, czyli jak narysować wykres funkcji liniowej?

By narysować wykres funkcji liniowej wystarczy wyznaczyć dwa punkty. Te dwa punkty to punkt przecięcia z osią OX i osią OY. Tak naprawdę mogą to być dwa jakiekolwiek punkty, ważne by się łączyły prostą kreską :).

Dziwisz się, że tylko dwa punkty są potrzebne?

Akurat przy funkcji liniowej mamy się fajnie, bo to zwykła prosta kreska i jedyne co musimy wiedzieć, to te dwa strategiczne punkty. Zobacz poniżej jak ja to wyznaczam.

Krok po kroku jak narysować wykres funkcji liniowej.

1. Rysujemy tabelkę.
2. wybieramy punkty dla których liczymy konkretne wartości
3. zaznaczamy punkty w układzie współrzędnych.
4. łączymy punkty prostą.
5. cieszymy się z wykresu.

Narysujmy wykres funkcji y = 2x+4.

Rysuję tabelkę.

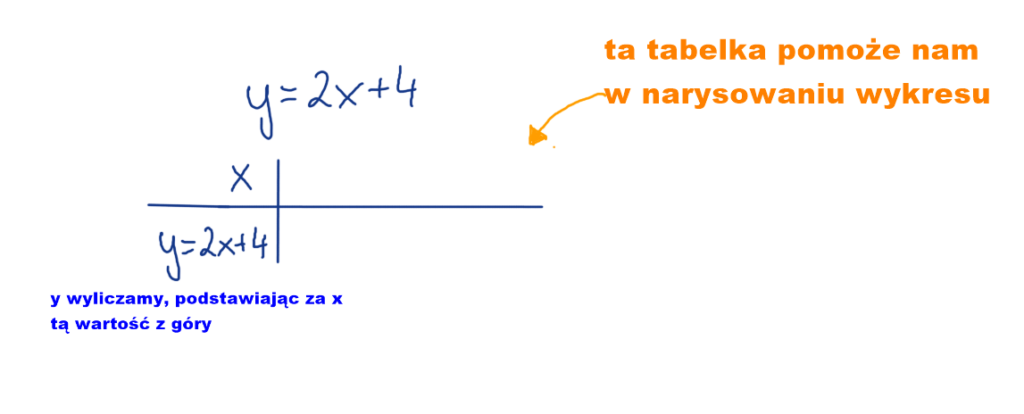
Teraz trzeba uzupełnić naszą tabelkę o podane wartości, więc spójrz na rysunek poniżej, tam wszystko wyjaśniłam co trzeba zrobić i jak.

Zbierzmy nasze punkty i zaznaczamy je w układzie współrzędnych.

Punkty, które mamy zaznaczyć na wykresie funkcji to:

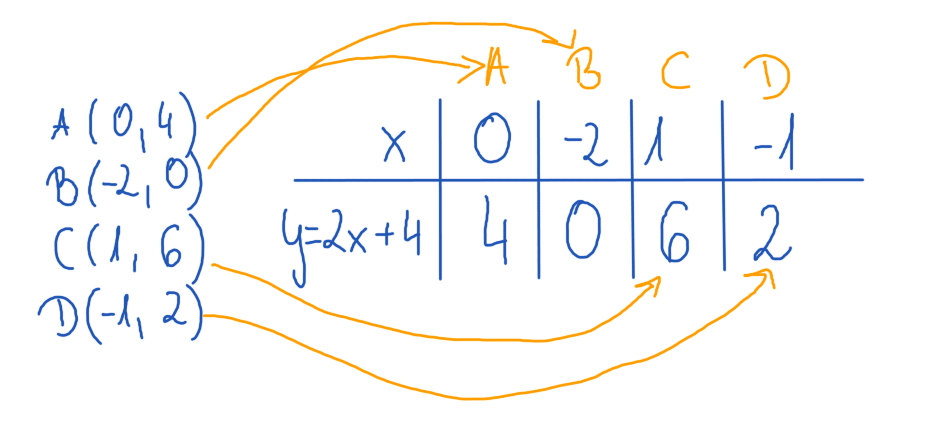
W układzie współrzędnych podane punkty wyglądają tak.

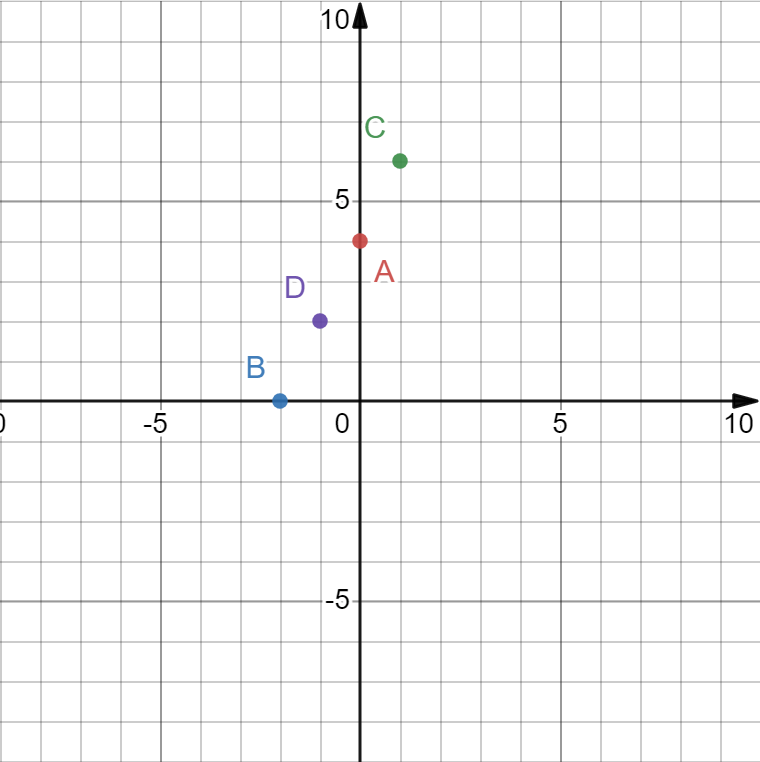
Gdy już je mamy teraz je łączymy prostą i otrzymujemy wykres funkcji liniowej.

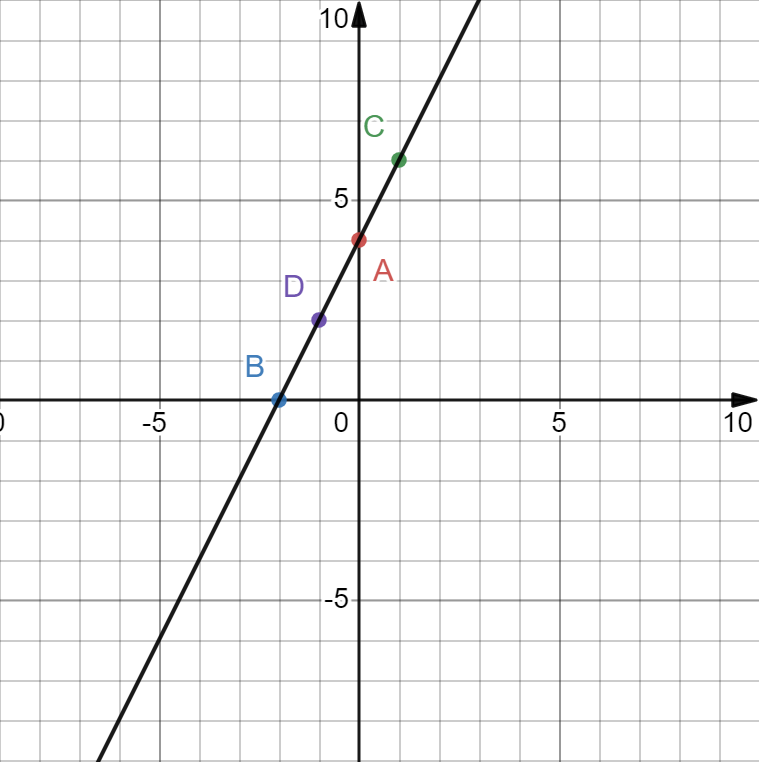
Więcej na ten temat poczytasz tutaj KLIK DO WPISU.

Monotoniczność funkcji liniowej.

Monotoniczność czyli inaczej zastanawiamy się kiedy funkcja jest rosnąca, malejąca lub stałą.

W funkcji liniowej jest to super fajne, ponieważ wszystko zależy od współczynnika kierunkowego, czyli od naszego a, inaczej mówiąc od tej liczby, która stoi przy x.

Funkcja liniowa jest :

• rosnąca gdy a>0,
• malejąca gdy a<0,
• stała gdy a=0.

Monotoniczność funkcji zadania do samodzielnej pracy.

Funkcja liniowa rosnąca.

By funkcja liniowa była rosnąca musi spełniać założenie, że a > 0. Pamiętaj, że a to ta liczba, która stoi przy x.

Przykłady funkcji liniowych rosnących.

Funkcja liniowa rosnąca na wykresie.

Funkcja liniowa rosnąca zadania do obliczenia. Zadania z parametrem.

Poniżej masz parę zadań do obliczenia, najpierw spróbuj sam a potem sprawdź wyniki ze mną. Powodzenia!

Funkcja liniowa malejąca.

I teraz gdy mówimy o funkcji liniowej malejącej, to wiemy, że ta funkcja ma a < 0, czyli ta liczba, która stoi przy x ma – przed brzuszkiem.

Przykłady funkcji liniowych malejących.

Funkcja liniowa malejąca na wykresie.

Funkcja liniowa malejąca zadania do obliczenia. Zadania z parametrem.

Poniżej masz parę zadań do obliczenia,w których masz sprawdzić kiedy nasza funkcja jest malejąca. Najpierw spróbuj sam a potem sprawdź wyniki ze mną. Powodzenia!

Funkcja liniowa stała.

To najlepsze, ze wszystkiego, bo gdy funkcja liniowa jest stała to nasze a=0 i wtedy we wzorze nie mamy x, ponieważ 0*x=0.

Przykłady funkcji liniowych stałych.

Funkcja liniowa stała na wykresie.

Funkcja liniowa stała w zadaniach z parametrem.

Kiedy funkcja liniowa jest stała? Co się dzieje gdy mamy parametr? Teraz czas na praktykę. Pamiętaj, funkcja liniowa stała, to taka funkcja, której współczynnik kierunkowy równa się 0.

Funkcja liniowa u mnie na kanale.

Jak zwykle ostatnim krokiem jaki Tobie podsuwam, pooglądania treści, które są u mnie na YouTube.

Podsumowanie – ściąga funkcja liniowa.

Funkcja liniowa to prosta, którą możemy spotkać pod dwiema postaciami:

• Postać kierunkowa y=ax+b,
• postać ogólna Ax + By + C= 0.

Dodatkowo by wyznaczyć punkt przecięcia funkcji liniowej z osią OX, za y podstawiamy 0 i wyliczamy wartość x, Jeśli nadal z tym nie czujesz się ok przeskocz tutaj KLIK lub zobacz film na YouTube KLIK W YT.

Z kolei by wyznaczyć punkt przecięcia funkcji liniowej z osią OY za z podstawiamy 0 i wyliczamy y. Pamiętaj, że jeśli funkcje liniową mamy przedstawioną za pomocą postaci kierunkowej, to wyraz wolny, czyli nasze b, jest tym punktem przecięcia z osią OY. Jeśli tutaj czujesz, że potrzebujesz jeszcze raz przeczytać o tym, to HOP w to miejsce, albo skok w YouTube.

Warte uwagi.

I tutaj ostro pracuję byś mogła / mógł poczytać super treści!