W świecie matematyki i statystyki, skala jest podstawowym pojęciem, które otwiera drzwi do zrozumienia wielu fascynujących koncepcji. Czy zastanawialiście się kiedykolwiek, jak to jest możliwe, że mimo olbrzymiego rozmiaru naszej planety, możemy łatwo zobaczyć jej obraz na małej mapie? Albo jak możemy tworzyć różne figury, które mimo różnicy w rozmiarach, zachowują takie same proporcje? Klucz do zrozumienia tych pytań leży właśnie w pojęciu skali, więc co to jest skala?
Skala podobieństwa figur i skala na mapie, chociaż stosowane w odmiennych kontekstach, mają wspólne podłoże. Oba te terminy odnoszą się do procesu, w którym coś zostało pomniejszone lub zwiększone pewną ilość razy, zachowując jednak proporcje pierwotne.
Przykładowo, jeżeli mówimy o skali na mapie, odnosimy się do stosunku odległości na mapie do rzeczywistej odległości na Ziemi. Ten stosunek pozwala nam na zmniejszenie olbrzymiej przestrzeni rzeczywistej do formatu przenośnej mapy, zachowując jednocześnie poprawność odległości między punktami.
Z drugiej strony, skala podobieństwa figur odnosi się do proporcjonalnej zależności między wymiarami dwóch figur. Na przykład, kwadrat o boku 4 cm jest w skali 1:2 w porównaniu do kwadratu o boku 2 cm. Innymi słowy, każdy wymiar większego kwadratu jest dwukrotnie większy od odpowiadającego mu wymiaru mniejszego kwadratu.
Zrozumienie skali jest kluczowe nie tylko dla nauki matematyki i geografii, ale ma również wiele praktycznych zastosowań w codziennym życiu – od projektowania domów po tworzenie modeli samochodów czy komputerowej grafiki 3D. Czy nie jest fascynujące, jak takie proste pojęcie jak skala może mieć tak wiele różnych zastosowań?
Teraz, kiedy zrozumiecie już podstawy, jestem pewna, że będziecie w stanie samodzielnie odkrywać i zrozumieć, jak skala jest wykorzystywana w różnych dziedzinach nauki i życia codziennego. Zapraszam do dalszego zgłębiania tego tematu!
Co to jest skala?
Skala informuje nas o tym, ile razy dane wymiary (długość odcinka) jednego obiektu (przedmiotu, drogi itp) są większe lub mniejsze od odpowiednich wymiarów drugiego.
Mówiąc inaczej skala to coś, co pomaga nam zrozumieć, jak duże lub małe są rzeczy w porównaniu do innych rzeczy. Wyobraźcie sobie, że macie model samochodu lub budynku. Skala mówi nam, ile razy musielibyśmy powiększyć ten model, aby stał się prawdziwym samochodem czy budynkiem.
Jeśli skala wynosi 1:100, to oznacza, że prawdziwy budynek jest 100 razy większy od modelu.
Lub pomyślcie o mapie. Skala na mapie mówi nam, ile razy długości na mapie są mniejsze od rzeczywistych długości na Ziemi. Jeśli skala na mapie wynosi 1:50 000, to oznacza, że 1 cm na mapie to tak naprawdę 50 000 cm, czyli 0,5 km w rzeczywistości. To jest bardzo pomocne, gdy chcemy zrozumieć, jak daleko od siebie są różne miejsca.
Skala jest też bardzo ważna w sztuce i rysunku. Dzięki niej artysta wie, jak duże lub małe powinny być rzeczy, które rysuje na obrazie, aby wszystko wyglądało realistycznie.
Więc, jak widzicie, skala jest naprawdę ważna w wielu różnych dziedzinach – od nauki przez sztukę, aż po nasze codzienne życie.
Bez skali, byłoby nam dużo trudniej zrozumieć i przedstawiać świat wokół nas.
Co oznacza skala 1 : 2 itp? Skala, która pomniejsza.
Zrozumienie skali może wydawać się nieco trudne, ale nie martwcie się – razem to rozwikłamy!
Skala, tak jak ta 1:2, 1:10, czy 1:100, która pomniejsza, mówi nam o relacji pomiędzy wielkością obiektu w rzeczywistości a jego reprezentacją, na przykład na rysunku czy w modelu.
Mówiąc wprost skala podobna w taki sposób, informuje nas o tym, że coś zostało pomniejszone o tyle razy ile wynosi ta druga liczba.
Ważne! Ta druga liczba musi być większa od tej pierwszej. Popatrz na rysunku poniżej zaznaczyłam, a jeszcze niżej masz przykłady.
Jeśli mówimy o skali 1:2, mamy na myśli, że każdy wymiar obiektu w rzeczywistości jest dwa razy większy niż na rysunku czy modelu.
To ważne, żeby pamiętać, iż druga liczba w skali musi być większa od pierwszej.
To dlatego, że mówimy o tym, ile razy obiekt jest pomniejszony – i pomniejszenie zawsze oznacza, że coś staje się mniejsze, prawda?
Na przykład, jeśli mamy domek dla lalki w skali 1:12. To oznacza, że wszystko w tym domku jest dwanaście razy mniejsze niż w prawdziwym domu. Czyli jeśli prawdziwe krzesło ma 60 cm wysokości, to krzesło dla lalki będzie miało 5 cm. Możemy to zobrazować na rysunku.
Weźmy dwa kwadraty. Jeden ma bok długości 2 cm, a drugi ma bok długości 4 cm. Skala między tymi kwadratami to 1:2, ponieważ bok drugiego kwadratu jest dwa razy dłuższy niż bok pierwszego kwadratu. Właśnie tak to działa!
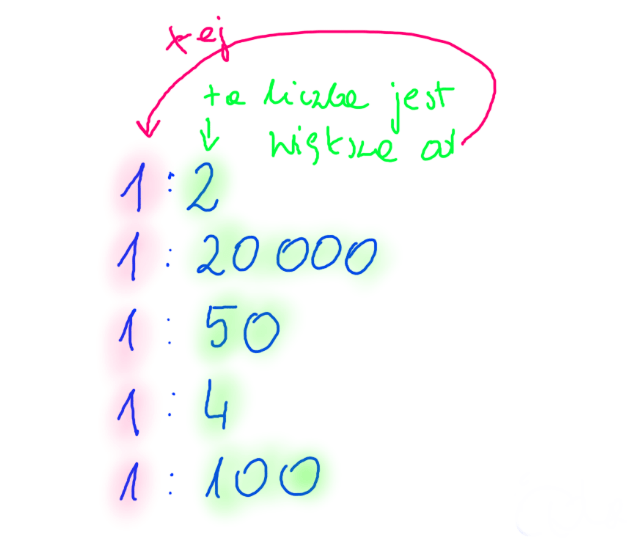
Przykłady do skali, która pomniejsza
- 1:2 Jeśli rysunek pewnego obiektu lub przedmiot został wykonany w skali 1:2, to oznacza, że na rysunku wymiary są dwukrotnie mniejsze niż w rzeczywistości.
- 1:20 000 Jeśli rysunek pewnego obiektu lub przedmiot został wykonany w skali 1:20 000, to oznacza, że na rysunku wymiary są dwadzieścia tysięcy razy mniejsze niż w rzeczywistości.
- 1:50 Jeśli rysunek pewnego obiektu lub przedmiot został wykonany w skali 1:50, to oznacza, że na rysunku wymiary są pięćdziesiąt razy mniejsze niż w rzeczywistości.
- 1:4 Jeśli rysunek pewnego obiektu lub przedmiot został wykonany w skali 1:4, to oznacza, że na rysunku wymiary są czterokrotnie mniejsze niż w rzeczywistości.
- 1:100 Jeśli rysunek pewnego obiektu lub przedmiot został wykonany w skali 1:100, to oznacza, że na rysunku wymiary są stukrotnie mniejsze niż w rzeczywistości.
Zadanie
Kwadrat 10 razy mniejszy jest narysowany w skali ?????
I tak 10 razy mniejszy, czyli muszę to zapisać o tak 1:10.
Więc nasze zdanie poprawnie będzie brzmiało tak:
Kwadrat 10 razy mniejszy jest narysowany w skali 1:10.
Zobacz podobne filmy.
Kliknij w obrazek i zacznij oglądać, lub czytaj dalej o skali, która pomniejsza.
Co oznacza skala 2 : 1 ? Skala, która powiększa.
Gdy widzisz skale 2:1, 10:1, 20000:1, 5:1, 50:1, zastanawiasz się, co one oznaczają?
Są to przykłady skali powiększającej.
Zasada jest prosta.
Pierwsza liczba przed dwukropkiem jest większa od drugiej.
To ona pokazuje, ile razy powiększamy dany obiekt.
Weźmy skale 2:1 jako przykład. Co ona oznacza? Jeżeli mamy model samochodu w tej skali, to prawdziwy samochód jest dwa razy większy. Zatem, skala 2:1 informuje nas, że rzeczywisty samochód jest dwa razy większy niż model.
Rozważmy inny przykład, skale 10:1. Jeśli masz na rysunku psa, którego długość wynosi 10 cm, to w skali 10:1 prawdziwy pies jest 10 razy większy, czyli mierzy 1 metr.
Inne skale, takie jak 20000:1, 5:1, 50:1, działają na tej samej zasadzie. Pierwsza liczba mówi nam, ile razy większy jest prawdziwy obiekt od jego reprezentacji.
To jest klucz do zrozumienia skali, która powiększa. Zawsze zwracaj uwagę na pierwszą liczbę – to ona mówi nam, ile razy powiększamy obiekt. To proste, prawda? Teraz, gdy już wiesz, jak działa skala powiększająca, możesz łatwiej zrozumieć różne modele, rysunki czy mapy, które często spotykasz na co dzień.
Przykłady zadań wraz z interpretacją podanej skali
- 2:1, jeśli rysunek pewnego obiektu lub przedmiot został wykonany w skali 2:1, to oznacza, że na rysunku wymiary są dwukrotnie zwiększony niż w rzeczywistości.
- 10:1, jeśli rysunek pewnego obiektu lub przedmiot został wykonany w skali 10:1, to oznacza, że na rysunku wymiary są dziesięciokrotnie większe niż w rzeczywistości.
- 20000:1, jeśli rysunek pewnego obiektu lub przedmiot został wykonany w skali 20000:1, to oznacza, że na rysunku wymiary są dwadzieścia tysięcy razy większe niż w rzeczywistości.
- 5:1, jeśli rysunek pewnego obiektu lub przedmiot został wykonany w skali 5:1, to oznacza, że na rysunku wymiary są pięć razy większe niż w rzeczywistości.
- 50:1, jeśli rysunek pewnego obiektu lub przedmiot został wykonany w skali 50:1, to oznacza, że na rysunku wymiary są pięćdziesięciokrotnie większe niż w rzeczywistości.
Zadanie
Kwadrat 10 razy większy jest narysowany w skali ?????
I tak 10 razy większy, czyli muszę to zapisać o tak 10:1.
Więc nasze zdanie poprawnie będzie brzmiało tak:
Kwadrat 10 razy większy jest narysowany w skali 10:1.
Skala na youtube: skala w praktyce.
Zachęcam do obejrzenia filmów, które wybrałam specjalnie dla Ciebie. Pokazują one, jak działa skala w praktyce. Wystarczy kliknąć na obrazek, a film zacznie się odtwarzać. To świetna okazja, by zobaczyć jak skala działa na żywo!
Nie zapomnij jednak kontynuować lektury. Dalej dowiesz się więcej o skali, która powiększa. To ważne, aby dobrze zrozumieć, jak działa. Bez tej wiedzy, może być trudno zinterpretować modele czy rysunki, które spotkasz w szkole czy na co dzień.
Więc kliknij na obrazek, zobacz film, a potem wróć tu, by dowiedzieć się jeszcze więcej. Czekam z dalszą porcją informacji!
Dziwnie zapisana skala. Jak to ogarnąć?
Masz zadanie a tam skala 2:3 albo 4:5 i co tutaj teraz zrobić?
Weźmy konkretny przykład.
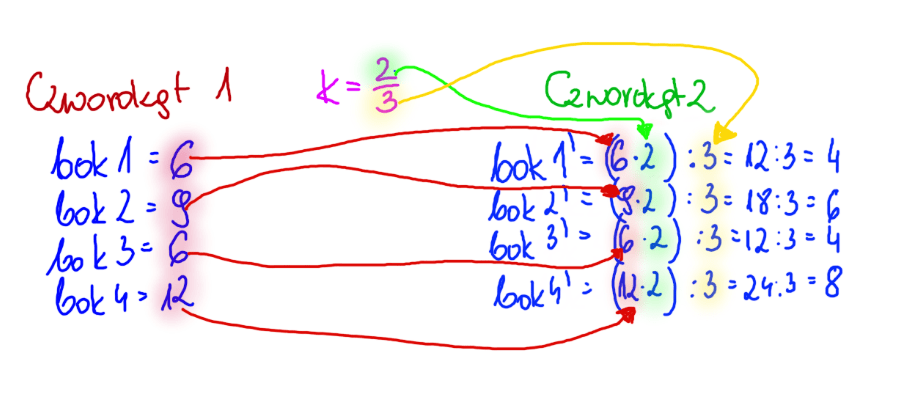
Czworokąty są podobne. Jeden ma boki długości 6,9,6,12. Oblicz długości boków drugiego, jeżeli skala podobieństwa wynosi 2:3.
Jak to zrobić?
Zacznijmy od wypisania danych.
Mamy dwa czworokąty, nazwijmy je:
- czworokąt 1 i oznaczę go jako C1
- i ma on boki o długości 6,9,6,12, mogę to też zapisać tak
- bok1=6
- bok2=9
- bok3=6
- bok4=12
- i ma on boki o długości 6,9,6,12, mogę to też zapisać tak
- czworokąt 2 i oznaczę go jako C2.
- jego boki musimy wyliczyć,
- wiemy, że ma 4 boki.
Są dwa sposoby by wyliczyć długości boków od czworokąta 2, bo na dwa sposoby można zastosować naszą skalę.
Pierwszy sposób.

Wiemy, że nasze oby dwa czworokąty są do siebie podobne w skali 2:3. Po prostu biorę długości boków czworokąta 1 i mnożę przez skalę, dzięki temu otrzymuję długości boków czworokąta 2.
Drugi sposób.
Aby znaleźć długości boków czworokąta w skali 2:3. Należy najpierw dany bok zwiększyć 2 razy a potem podzielić na 3.
Co oznacza skala 1:1? Figury przystające.
Gdy mamy dwie figury – powiedzmy, dwa trójkąty, dwa kwadraty lub jakiekolwiek inne wielokąty – narysowane w skali 1:1, to mówimy, że są one identyczne. Skala 1:1 pokazuje nam, że wszystkie wymiary jednej figury są dokładnie takie same jak wymiary drugiej figury.
Innymi słowy, jeśli weźmiemy miarkę i zmierzymy długość boków, przekątnych, kątów, wysokości – cokolwiek to jest – wszystko to będzie takie samo w obu figurach. Dlatego, gdy widzisz skale 1:1, możesz być pewien, że figury są identyczne.
W matematyce, gdy mówimy, że dwie figury są takie same, używamy słowa „przystające”. To specjalne słowo, które oznacza, że wszystkie kąty i długości boków są takie same. Czyli, gdy mówimy, że figury narysowane w skali 1:1 są przystające. Mamy na myśli, że są one identyczne pod względem kształtu i rozmiaru.
Czy to nie jest fascynujące? Matematyka jest pełna takich niesamowitych faktów. Pamiętaj o tym, gdy następnym razem zobaczysz dwie figury narysowane w skali 1:1. To oznacza, że są one przystające, czyli takie same!
Podsumowanie – to zapamiętaj o figurach przystających.
Jeśli dwie figury np. dwa wielokąty, dwa trójkąty itd. są narysowane w skali 1:1, to oznacza, że są takie same.
Figury narysowane w skali 1:1 mówimy, że są przystające.
Podsumowanie.
Skala informuje nas o tym ile razy zwiększyliśmy lub powiększyliśmy jakiś obiekt, odcinek itd. względem oryginału.
Kiedy zmniejszamy?
Zmniejszamy gdy mamy skalę podaną w taki sposób 1:15, 1:56, 1: 10000.
Mam figure F1 i jest ona podobna do figury F2 w skali 1:5. Oznacza to, że każdy bok figury F1 muszę pomnożyć przez 1/5, by otrzymać boki figury F2. Mówiąc jeszcze inaczej każdy bok figury F1 musze podzielić przez 5 by otrzymać konkretne boki figury F2.
Zmniejszamy jak mam podana skalę w taki sposób, że liczba przed dwukropkiem jest mniejsza od liczby za dwukropkiem.

A kiedy zwiększamy?
I teraz spójrzmy na podobny problem. Mamy dwie figury podobne F1 i F2 ale skala podobieństwa wynosi 5:1. Oznacza to, że każdy bok figury F1 mnożymy przez 5 i otrzymujemy bok figury F2. I już.
Zwiększamy jak mam podana skalę w taki sposób, że liczba przed dwukropkiem jest większa od liczby za dwukropkiem.

Chciałam w jednym wpisie wrzucić też o skali na mapie, ale bardzo długi ten wpis się zrobił zatem zapraszam Ciebie tutaj byś przeczytał.a o skali na mapach.
A gdy chcesz wiedzieć więcej o figurach podobnych to możesz przeczytać tutaj albo o trójkątach podobnych tutaj.
I to już na tyle.
Buziaki!









