W tym roku oficjalna matura próbna z matematyki podstawowej z Centralnej Komisji Edukacyjnej odbyła się w marcu 2021 roku.
Wszyscy długo na nią wyczekiwaliśmy, bo każdy był ciekawy zadań. Wiadomo, że kilka zagadnień wyleciało z tego rocznej matury.
Matura próbna z CKE to co innego niż matura próbna z Operonu czy Nowej Ery. Jest bardziej stresująca i dostarcza więcej emocji niż matury próbne od wydawnictw.
Poniżej wrzucam listę zadań z tegorocznej matury próbnej wraz z informacjami jakie umiejętności musisz posiadać by ją zrobić. Może lepiej powiedzieć jaką wiedzę musisz mieć. O! Albo z tipami jak to zrobić.
Dodatkowo będę Ciebie odsyłać do rozwiązań – jak się okaże, że nie masz pomysłu jak to zadanie zrobić.

By zrobić to zadanie nie możesz się bać pierwiastków 🙂
Musisz znać wzory skróconego mnożenia (!!! w tablicach maturalnych są one wszystkie !!!). Jeśli dostajesz zawału serca przy nich zerknij TUTAJ – tam znajdziesz wytłumaczone jak korzysta się ze wzorów skróconego mnożenia i jak jej się wykorzystuje.
Skorzystać trzeba z tego wzoru:
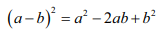
Później redukujemy wyrazy podobne i już.
I tyle.
Rozwiązanie znajdziesz TUTAJ.

W tym zadaniu sprawdzają Twoje umiejętności odnośnie logarytmów. Wzory na logarytmy znajdziesz w tablicach maturalnych, które możesz mieć na maturze. Jeśli gubisz się przy obliczaniu logarytmu to powtórz ten materiał, możesz znaleźć TUTAJ powtórkę, gdzie liczę logarytm korzystając z jego definicji czy właśnie tych wzorów na logarytm, które znajdziesz w tablicach maturalnych.
By obliczyć to zadanie to najpierw musisz skorzystać z tego wzoru:
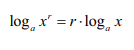
I dzięki temu temu pozbędziemy się 2 sprzed 2log5 z 4 i 3 sprzed log5 z 1/2.
Jak już to zrobisz, to teraz trzeba skorzystać z tego wzoru:
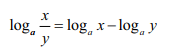
I to już koniec zadania.
Rozwiązanie znajdziesz TUTAJ.

Rozwiązać to zadanie możesz dzięki proporcji.
Wskutek podwyżki zdrożała o 40% czyli aktualnie płacimy 140% ceny. 140% dlatego, że przed podwyżką cena maseczki to 100% jak sklep zrobił podwyżkę to znaczy, że musimy zapłacić więcej o tyle % o ile zrobili właśnie podwyżkę, dlatego mamy 100% (czyli stara cena, cena przed podwyżką) + 40% (czyli ta podwyżka) = 140%.
I w zadaniu nam powiedzieli, że ta cena to 106,40 zł.
I co mi to wszystko daje?
x to 100%
106,40 to 140%
I robię proporcję, czyli mnożę na skos.
I tyle.
Jeśli to dla Ciebie brzmi jak padaka, rozwiązanie znajdziesz tutaj.
A jeśli nie lubisz procentów to powtórkę znajdziesz tutaj.

Łooooo jacie… pierwiastki, potęgi i do tego na maturze… Jak to ugryźć, jak to rozwiązać?
Najpierw trzeba nasze pierwiastki zamienić na potęgę. Korzystamy tutaj z tego wzoru:
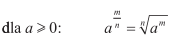
Gdy już to zrobimy to teraz korzystamy z kolejnego wzoru:
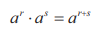
I jak już sobie dodamy wykładniki, to korzystamy ze wzoru na potęgę potęgi:
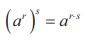
Jeśli dla Ciebie to brzmi jak zaklęcia, rozwiązanie znajdziesz tutaj.
Jeśli nie cierpisz potęg i jak je widzisz to masz ochotę puścić pawia na zadanie, to tutaj znajdziesz wszystko na temat potęg, od samego początku, prościutkich, przyjemniutkich przykładów do bardziej zaawansowanych i nie miłych dla oka 🙂


