Zaokrąglanie liczb lub przybliżenie, wykorzystujemy bardzo często w życiu codziennym. Ile razy mówimy to kosztuje prawie 100 zł (cena 99,90 zł) itp. Dziś pokażę jak to wygląda od strony matematycznej.

Zaokrąglanie liczb lub przybliżenie liczb przerabiane jest teraz w 7 klasie szkoły podstawowej. Tutaj można zobaczyć np. podręcznik w formie on-line. Klikając w słowo tutaj od razu przeniesiesz się na stronę w podręczniku dotyczącą zaokrąglania liczb.

Nie będę przepisywać teorii, bo nie o to mi chodzi. Teoria – teorią, praktyka – praktyką.

Przejdę od razu do części praktycznej. Tak najlepiej zrozumieć o co chodzi z całym zaokrąglaniem.

Zaokrąglanie liczb jest związane ze znajomością poniższej tabelki, czyli wiemy która to jest cyfra setek, cyfra tysięcy, czy która cyfra stoi na miejscu części setnej.

Przykład 1.

Zaokrąglij podaną liczbę do setek.

a) 986 442

b) 986 492

Rozwiązanie.

Po patrz dwa przykłady, prawie niczym się nie różnią.

A jednak, ta subtelna różnica robi wiele. Miesza wiele.

Stań i popatrz.

Przykład A 

986442

Przykład B

986492

Liczby różnią się tylko w miejscu gdzie cyfrę zaznaczyłam na czerwono. 

Jeszcze raz wrzucę.

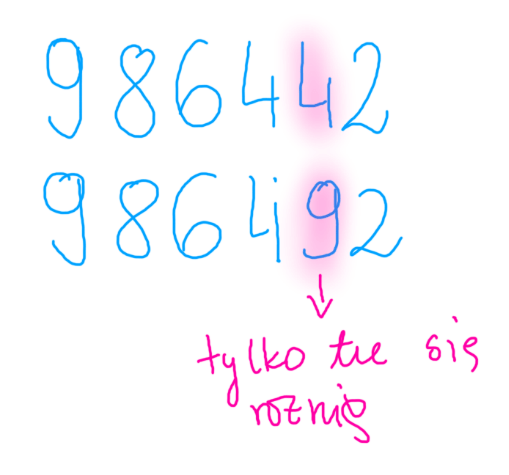
Teraz wyjaśnie jak wielkie ma znaczenie ta różnica i o co chodzi z tym zaokrąglaniem do setek.

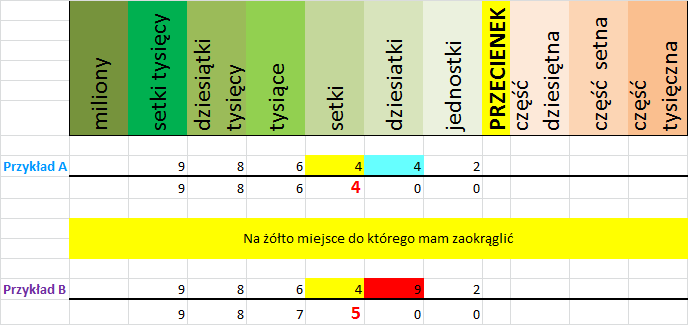
Krok po kroku jak zaokrąglić daną liczbę

1. Czytasz treść zadania i patrzysz do której liczby masz zaokrąglić, np. do setnych.
2. W kolejnym kroku patrzysz na liczbę po prawej od tej cyfry do której masz zaokrąglić, w naszym przykładzie przybliżaliśmy do setnych to patrzę na dziesiątki. Tak na prawo od setnych są dziesiątki.
3. Jeśli ta cyfra z prawej jest większa od 5 to muszę dodać 1 do setnej, jeśli mniejsza zostawiam to bez zmian.
4. Przeczytaj jeszcze raz te kroki i przykład powyżej.
5. Lub popatrz jeszcze na przykłady poniżej, tam mówię bardziej ludzkim głosem.

Zadanie 1.

Zaokrąglij liczbę z podaną dokładnością
257 893,452    

a) do tysięcy
b) do setek
c) do dziesiątek
d) do liczby całkowitej
e) do częsci dziesiętnej
f) do części setnej

Rozwiązanie.

Uwaga! Cyfrę na czerwono mamy zaokrąglić (przybliżyć), a na cyfrę zaznaczoną na niebiesko patrzę by wiedzieć co zrobić z czerwoną.

a) zaokrąglamy 257 893,452 do tysięcy

Zaokrąglanie liczb do tysięcy – najpierw pomyślmy, jaka cyfra stoi na miejscu tysięcy.

257 893,452 ≈ 258 000,000

Jeśli po cyfrze zaokrąglanej znajduje się 5,6,7,8 albo 9 to zaokrąglamy w górę.

Tłumaczą na człowieczy język:

• zaokrąglamy do tej cyfry co jest na czerwono zaznaczone 7, tam właśnie się mówi, że zaokrąglam lub przybliżam do tysięcy, lub też spotkasz się z nazwą cyfra tysięcy.
• Tak 7 jest cyfrą tysięcy
• za tą cyfrą stoi 8 i to 8 jest większe od 5
• czyli do czerwonego 7 muszę dodać 1 , czyli cyfrę tysięcy zwiększam o 1.
• i w miejsce czerwonej 7 wskakuje 8 (bo patrz kropka wyżej 7+1=8) i przybliżenie mam 258 000

b) zaokrąglamy 257 893,452 do setek

Zaokrąglanie liczb do setek – najpierw pomyślmy, jaka cyfra stoi na miejscu setek.

257 893,452 ≈ 257 900,000

Jeśli po cyfrze zaokrąglanej znajduje się 5,6,7,8 albo 9 to zaokrąglamy w górę.

Tłumaczą na człowieczy język:

• zaokrąglamy do tej cyfry co jest na czerwono zaznaczone 8, tam właśnie się mówi, że zaokrąglam lub przybliżam do setek, lub też spotkasz się z nazwą cyfra setek.
• Tak 8 jest cyfrą setek
• za tą cyfrą stoi 9i to 9 jest większe od 5
• czyli do czerwonego 8 muszę dodać 1 , czyli cyfrę setek zwiększam o 1.

c) zaokrąglamy 257 893,452 do dziesiątek

Zaokrąglanie liczb do dziesiątek – najpierw pomyślmy, jaka cyfra stoi na miejscu dziesiątek.

257 893,452 ≈ 257 890,000

Jeśli po cyfrze zaokrąglanej znajduje się 0,1,2,3 albo 4 to zaokrąglamy w dół.

Tłumaczą na człowieczy język:

• zaokrąglamy do tej cyfry co jest na czerwono zaznaczone 9, tam właśnie się mówi, że zaokrąglam lub przybliżam do dziesiątek, lub też spotkasz się z nazwą cyfra dziesiątek.
• Tak 9 jest cyfrą dziesiątek
• za tą cyfrą stoi 3 i to 3 jest mniejsze od 5
• czyli nie zmieniam naszej liczby, a za 3 daję 0.

d) zaokrąglamy 257 893,452 do liczby całkowitej

Zaokrąglanie liczb do liczby całkowitej – najpierw pomyślmy, jaka cyfra stoi na miejscu jednostki.

257 893,452 ≈ 257 893,000

Jeśli po cyfrze zaokrąglanej znajduje się 0,1,2,3 albo 4 to zaokrąglamy w dół.

Tłumaczą na człowieczy język:

• zaokrąglamy do tej cyfry co jest na czerwono zaznaczone 3, tam właśnie się mówi, że zaokrąglam lub przybliżam do liczby całkowitej
• jak zaokrąglam do liczby całkowitej to patrzę co stoi zaraz za przecinkiem
• za tą przecinkiem stoi cyfra 4 i to 4 jest mniejsze od 5
• czyli nie zmieniam naszej liczby i za liczby po przecinku wpisuje 0

e) zaokrąglamy 257 893,452 do części dziesiętnej

Zaokrąglanie liczb do części dziesiętnej- najpierw pomyślmy, jaka cyfra stoi na miejscu części dziesiętnej.

257 893,452 ≈ 257 893,500

Jeśli po cyfrze zaokrąglanej znajduje się 5,6,7,8 albo 9 to zaokrąglamy w górę.

Tłumaczą na człowieczy język:

• zaokrąglamy do tej cyfry co jest na czerwono zaznaczone 4, tam właśnie się mówi, że zaokrąglam lub przybliżam do części dziesiętnej lub do jednego miejsca po przecinku
• jak zaokrąglam do jednego miejsca po przecinku patrzę na drugą liczbę po przecinku, czyli na 5
• 5 jest równe 5, 
• czyli do czerwonej 4 muszę dodać 1 

f) zaokrąglamy 257 893,452 do części setnej

Zaokrąglanie liczb do części setnej- najpierw pomyślmy, jaka cyfra stoi na miejscu części setnej.

257 893,452 ≈ 257 893,450

Jeśli po cyfrze zaokrąglanej znajduje się 0,1,2,3 albo 4 to zaokrąglamy w dół.

Tłumaczą na człowieczy język:

• zaokrąglamy do tej cyfry co jest na czerwono zaznaczone 5, tam właśnie się mówi, że zaokrąglam lub przybliżam do części setnej lub do drugiego miejsca po przecinku
• jak zaokrąglam do drugiego miejsca po przecinku patrzę na trzecią liczbę po przecinku, czyli na 2
• 2 jest mniejsze od 5
• czyli nie zmieniam naszej liczby i za liczby po przecinku wpisuje 0

I to na tyle 

Pozdrawiam

Ola