W pierwszej klasie liceum/technikum, gdzieś w okolicach drugiego semestru zaczynasz dział o szumnej nazwie funkcje. Funkcje to dział wprowadzający w szeroki temat jakim są funkcje w matematyce. Różnych funkcji jest dosyć sporo i o nich wszystkich będziesz się uczyć, aż do zakończenia edukacji. By nie mieć problemów z funkcją w szkole, wystarczy zrozumieć co to jest funkcja w matematyce.

Dział o funkcjach porusza takie tematy jak:

• czym są funkcje, czyli definicja funkcji,
• co to jest dziedzina funkcji i jak się nią wyznacza,
• co to jest zbiór wartości,
• jak znaleźć miejsce zerowe funkcji, czyli punkt przecięcia z osią OX,
• jak wyznaczyć monotoniczność funkcji, czyli kiedy funkcja jest rosnąca, a kiedy jest malejąca,
• ekstrema funkcji, czyli jej największa i najmniejsza wartość,
• przekształcenia wykresu funkcji.

Jeśli ogarniesz te powyższe tematy tak, że mucha nie siada to nie będziesz mieć problemu przez całe liceum czy technikum, bo te informacje są uniwersalne i działają tak samo w każdej funkcji. Mam tu na myśli, że jak zrozumiesz co to jest dziedzina funkcji i jak się ją wyznacza to bez problemu wyznaczysz dziedzinę funkcji dla konkretnej funkcji, np. liniowej, kwadratowej, logarytmicznej, wymiernej itp. itd.

Ale dobra, basta, stop!

Chcesz dowiedzieć się co to jest funkcja, no to już lecimy z tym tematem.

Funkcja w matematyce.

Definicja:

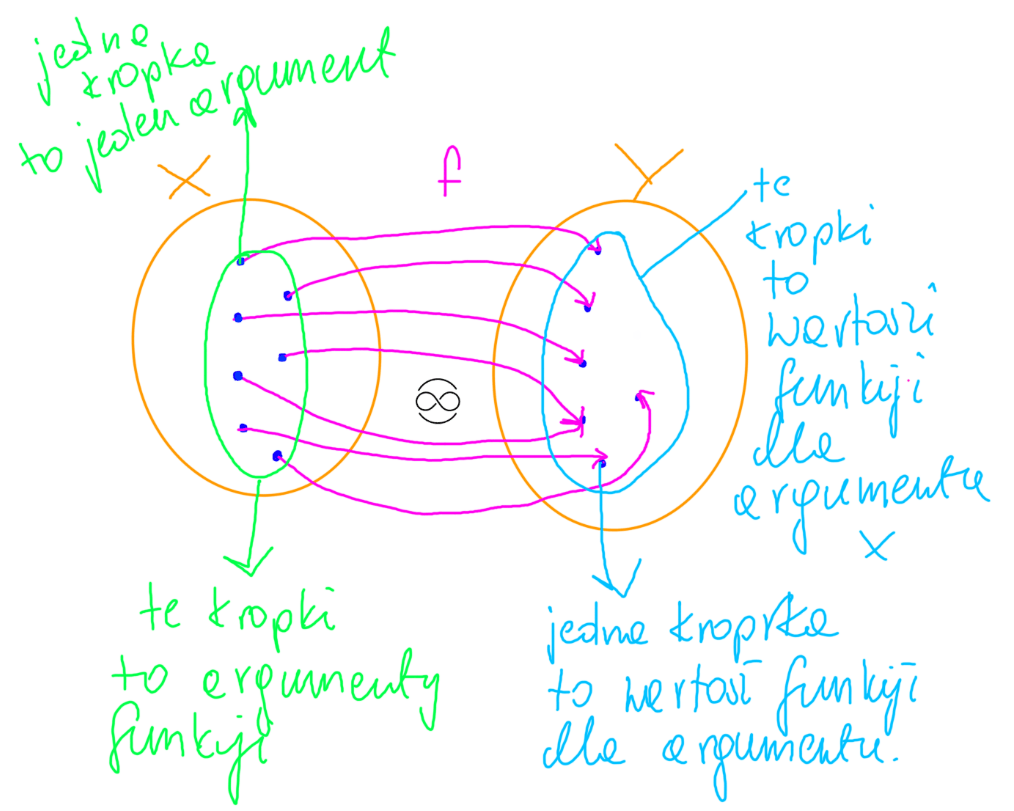
Funkcją f określoną na zbiorze X o wartościach w zbiorze Y nazywamy takie przyporządkowanie, które każdemu elementowi ze zbioru X przyporządkowuje dokładnie jeden element zbioru Y.

I teraz co tutaj jest najważniejsze w tej definicji.

Najważniejsze jest to zdanie.

„przyporządkowanie, które każdemu elementowi ze zbioru X przyporządkowuje dokładnie jeden element zbioru Y.”

Oznacza to, że biorę jeden element zbioru X i łącze go tylko, i wyłącznie z jednym elementem zbioru Y.

A oto przykład.

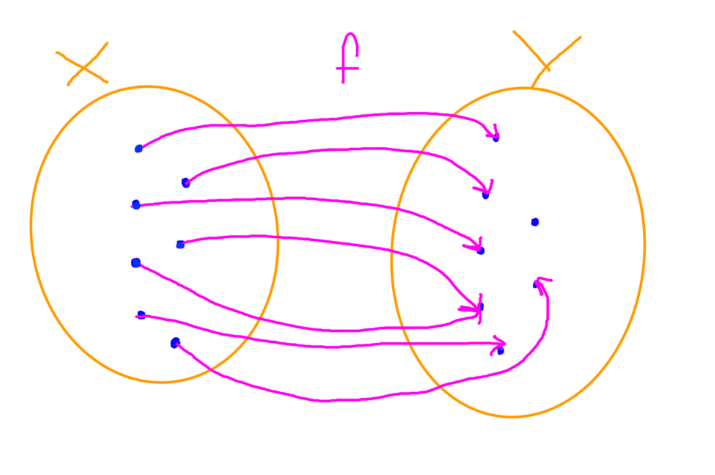
Elementy, które są w zbiorze X, to są argumenty funkcji.

Elementy, które są w zbiorze Y, to są wartości funkcji dla argumentu X.

Mówiąc prościej:

• argument funkcji to iks.
• wartość funkcji to igrek.

Jak możemy przedstawić funkcję? Metody przedstawiania funkcji.

Jest kilka metod przedstawienia funkcji. Z każdą z nich na pewno nie raz się spotkałeś i nie miałeś bladego pojęcia, że to jest funkcja. Pojęcie funkcji otacza nas każdego dnia, lecz niestety na to uwagi nie zwracam, bo też i po co ;).

Funkcję można przedstawić za pomocą:

• Opisu słownego,
• grafiki,
• tabelki,
• zbioru uporządkowanych par,
• wzoru,
• wykresu.

Przykład opisu słownego funkcji:

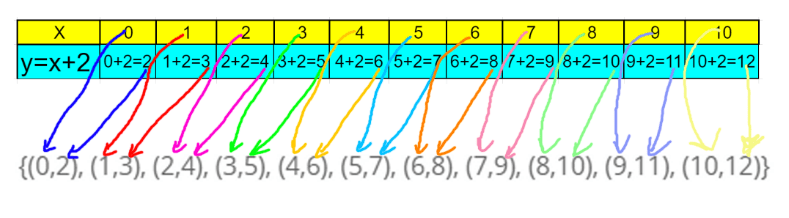
Funkcja f przyporządkowuje każdej liczbie ze zbioru X= {0,1,2,3,4,5,6,7,8,9,10} liczbę o 2 od niej większą.

Przykład funkcja przedstawiona za pomocą grafu:

Powyższy przykład przedstawię za pomocą grafu.

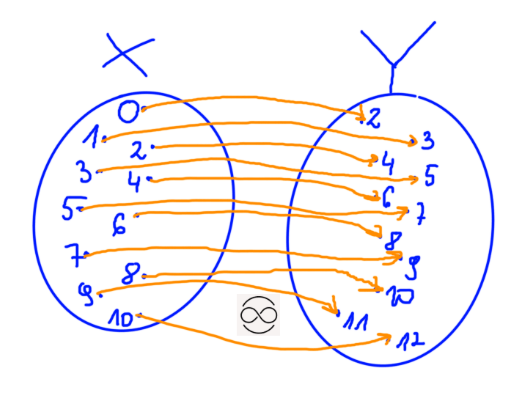
Przykład: funkcja przedstawiona za pomocą tabeli:

Przykład: funkcja przedstawiona za pomocą zbioru uporządkowanych par:

{(0,2), (1,3), (2,4), (3,5), (4,6), (5,7), (6,8), (7,9), (8,10), (9,11), (10,12)}

Jak to zrobić i skąd się wzięły te liczby w nawiasie, odpowiedź na te pytania znajdziesz poniżej.

Przykład: funkcja przedstawiona za pomocą wzoru:

Można zrobić to na parę sposobów, na przykład tak:

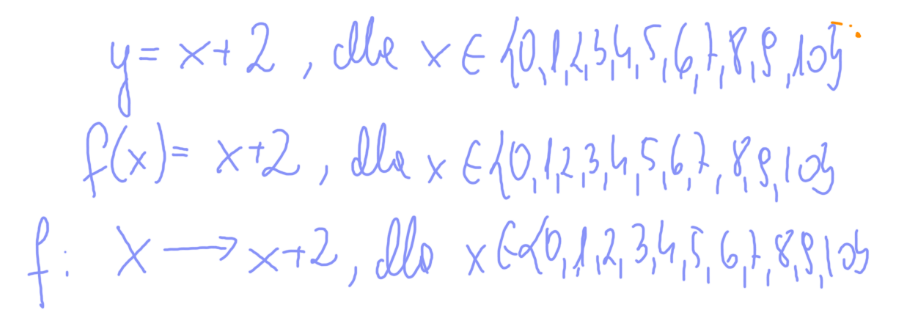
Najtrudniejsze w przedstawieniu funkcji za pomocą wzoru jest zauważenie tego wzoru. Jeśli funkcja jest w treści zadania opisana za pomocą opisu słownego (tak jak w naszym przypadku), to wystarczy zamienić słowa na znaki z matematyki.

Funkcja f przyporządkowuje każdej liczbie ze zbioru X= {0,1,2,3,4,5,6,7,8,9,10} liczbę o 2 od niej większą. Tak mamy w treści zadania. Liczba o 2 od niej większa, czyli po prostu x (to nasza liczba ze zbioru X) + 2 (bo o dwa większa, czyli musimy dodać 2 do naszej liczby ze zbioru X).

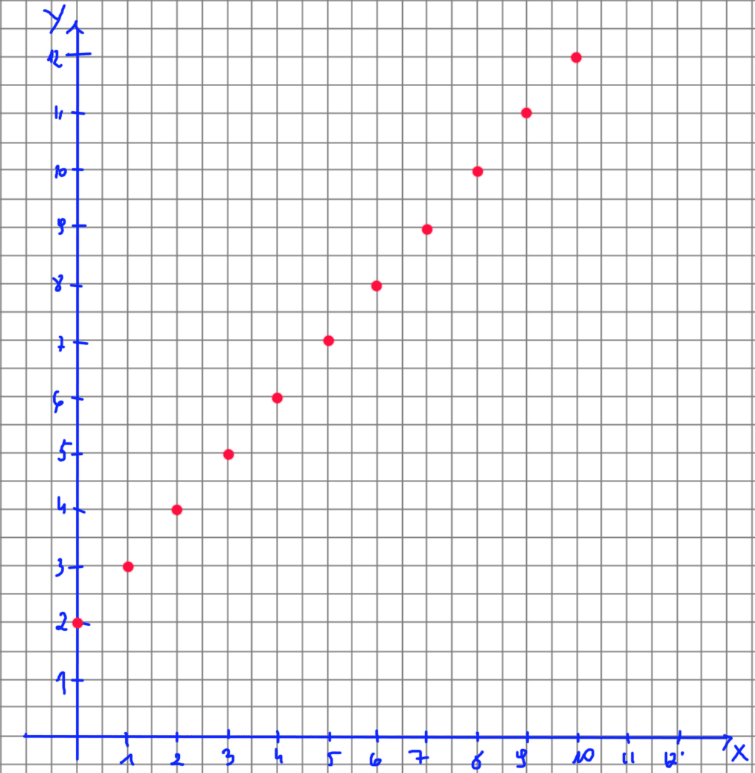
Przykład: funkcja przedstawiona za pomocą wykresu:

By przedstawić funkcję za pomocą wykresu, wystarczy zaznaczyć odpowiednie punkty w układzie współrzędnych.

Zadanie.

Który z poniższych wykresów przedstawia funkcję?

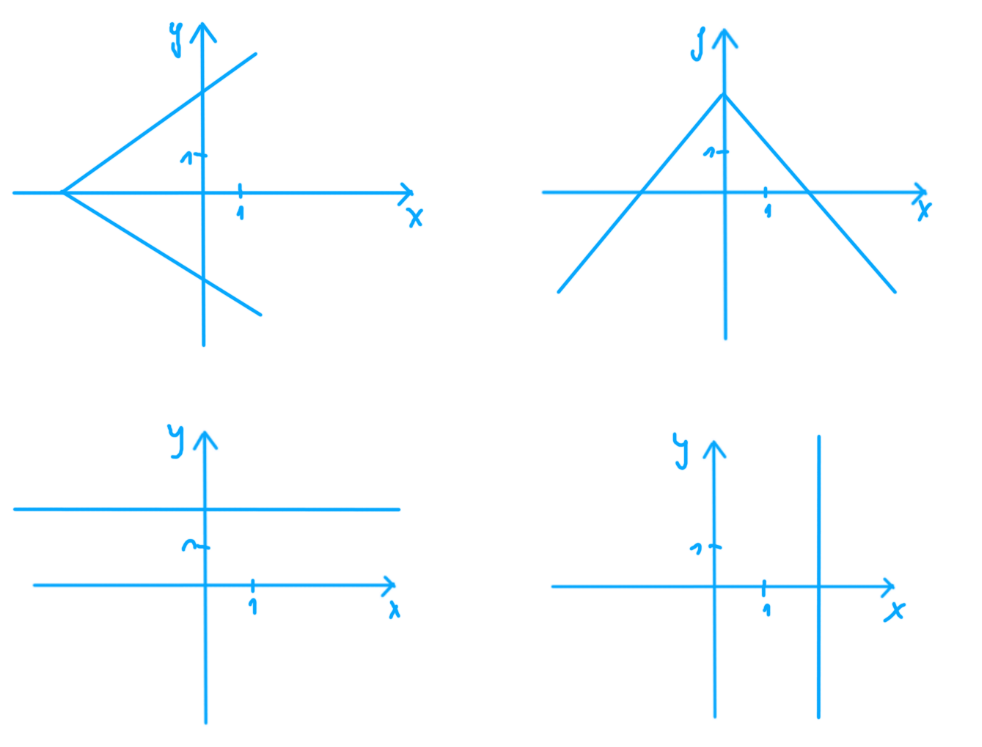
Rozwiązując to zadanie, pamiętaj o definicji funkcji oraz o najważniejszym jej zdaniu „przyporządkowanie, które każdemu elementowi ze zbioru X przyporządkowuje dokładnie jeden element zbioru Y.”

Dziś będę wstręciuch i rozwiązanie podaje Tobie tutaj.

Skąd mam wiedzieć, że coś nie jest funkcją? Kiedy? Jak?

Teraz pora na zagadki.

Zagadka 1.

Który z poniższych grafów NIE przedstawia funkcji?

Odpowiedź. Graf numer 2 przedstawia funkcję. Grafy numer 1,3,4 nie przedstawiają funkcji.

W tym miejscu możesz posłuchać jak wyjaśniam ten przykład, oczywiście dorzucam kilka grafów gratis, więc zamiast 4 grafów, omawiam 6 :), zapraszam Ciebie w to miejsce, o TUTAJ ZRÓB KLIK.

Zagadka 2.

Która z poniższych tabelek NIE przedstawia funkcji?

Dodam wkrótce.

Zagadka 3.

Która z poniższych par uporządkowanych NIE przedstawia funkcji?

Dodam wkrótce.

Zagadka 4.

Podeślij mi swój przykład na niefunkcję.

Zapraszam Ciebie do zagłębienia wiedzy z funkcji.

1. Dziedzina funkcji.
2. Zbiór wartości funkcji.
3. Miejsce zerowe funkcji.
4. Monotoniczność funkcji.
5. Przekształcenie wykresu funkcji.
   • względem osi OY,
   • względem osi OX,
   • przesunięcie o wektor,
   • symetria względem osi OX,
   • symetria względem osi OY,
   • wartość bezwzględna,
   • mix wszystkiego.

Jak masz jakieś pytania czy wątpliwości to pisz, np. przez formularz kontaktowy o tutaj.